Помогите решить пример во выш мату срочно

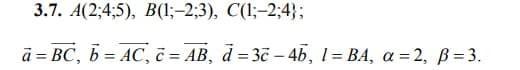
Ответы
1) Находим вектор a = BC = (1-1; -2-(-2); 4-3) = (0; 0; 1).
его модуль равен 1.
Находим вектор b = AC = (1-2; -2-4; 4-5) = (-1; -6; -1).
Скалярное произведение ab = 0*(-1) + 0*(-6) + 1*(-1) = -1.
2) Находим вектор c = AB = (1-2; -2-4; 3-5) = (-1; -6; -2).
Модуль c = √((-1)² + (-6)² + (-2)²) = √(1 + 36 + 4) = √41.
Косинус угла ϕ = (a_c) = (0*(-1) + 0*(-6) + 1*(-2))/(1*41) = -2/√41 = -2√41/41.
Угол ϕ = arccos(-2√41/41) = 108,201 градуса.
3) Орт вектора d равен: e = d/|d|.
Находим вектор d и его модуль.
d = 3c – 4b = 3*(-1; -6; -2) – 4*(-1; -6; -1) = (-3+4; -18+24; -6+4) = (1; 6; -2).
Модуль равен √(1² + 6² + (-2)²) = √(1 + 36 + 4) = √41.
Подставим данные в формулу.
е = ((1/√41); (6/√41); (-2/√41)).
4) Координаты точки делящей отрезок в данном соотношении находятся по формулам:
x = βx1+αx2 = x1+λx2
α+β 1+λ
y = βy1+αy2 = y1+λy2
α+β 1+λ
z = βz1+αz2 = z1+λz2
α+β 1+λ
Подставим координаты концов отрезка l = ВА в формулу при α = 2, β = 3.
Первая точка В(1; -2; 3), вторая А(2; 4; 5).
x(M) = (3*1 + 2*2)/(2 + 3) = 7/5 = 1,4.
y(M) = (3*(-2) + 2*4)/(2 + 3) = 2/5 = 0,4.
z(M) = (3*3 + 2*5)/(2 + 3) = 19/5 = 3,8.
5) Площадь параллелограмма равна модулю векторного произведения.
Векторное произведение a = (0; 0; 1), b = (-1; -6; -1):
i j k
0 0 1
-1 -6 -1 =
=i(0·(-1)-1·(-6)) - j(0·(-1)-1·(-1)) + k(0·(-6)-0·(-1)) = 6i - 1j - 0k.
S =√(6² + (-1)² + 0²) = √(36 + 1 + 0) =√37 ≈ 6,0828.