МАТРИЦА 70 БАЛЛОВ
НАЙТИ РЕШЕНИЕ можно через алгоритм Гауса
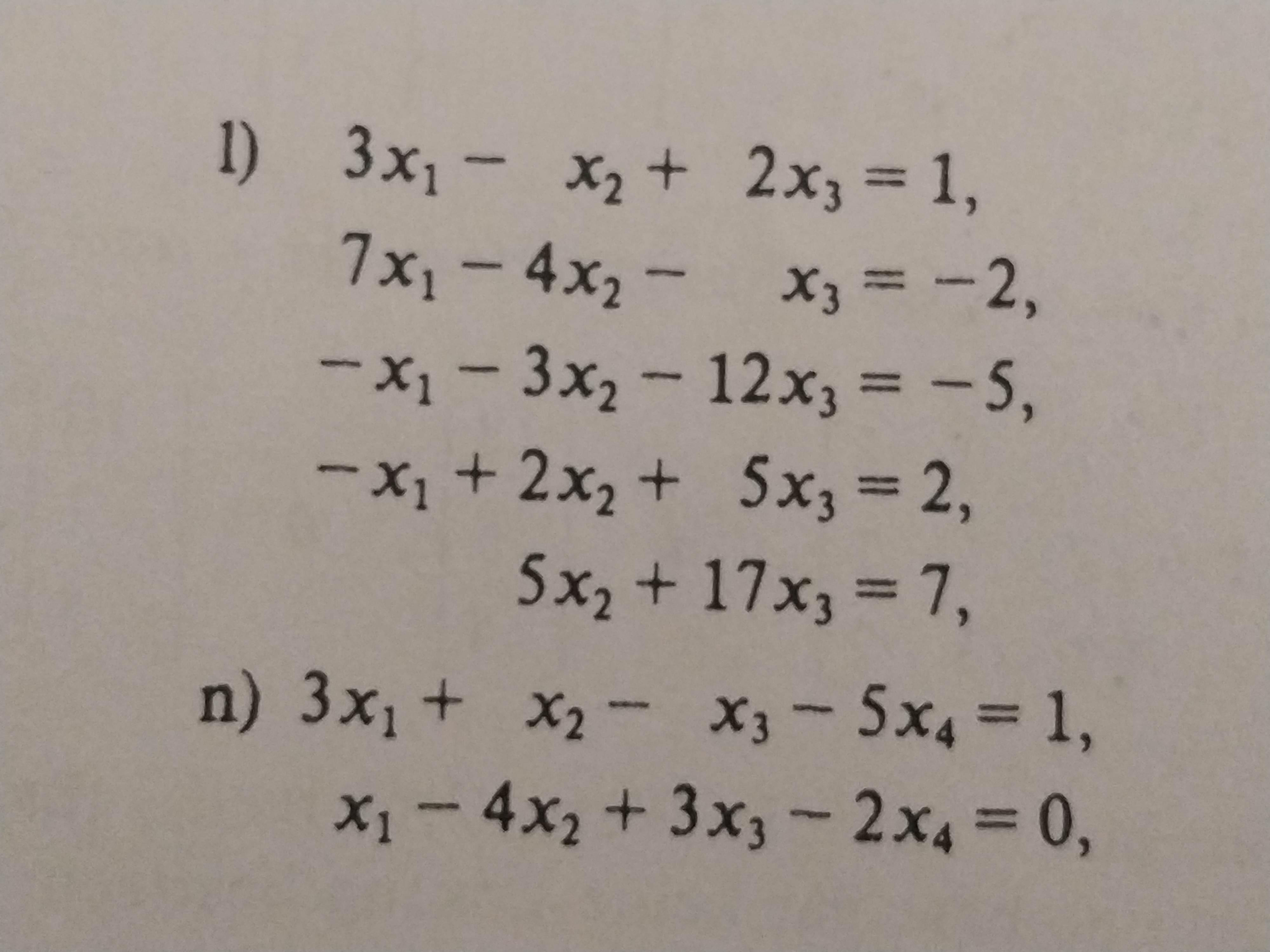
Ответы
Ответ:
P.S. Идет x1 x2 x3 x4 = B
1)
Запишем систему в виде расширенной матрицы:
3 -1 2 1
7 -4 -1 -2
-1 -3 -12 -5
-1 2 5 2
0 5 17 7
Для удобства вычислений поменяем строки местами:
0 5 17 7
-1 -3 -12 -5
-1 2 5 2
3 -1 2 1
7 -4 -1 -2
Умножим 3-ю строку на (-1). Добавим 3-ю строку к 2-й:
0 5 17 7
0 -5 -17 -7
-1 2 5 2
3 -1 2 1
7 -4 -1 -2
Умножим 3-ю строку на (3). Добавим 4-ю строку к 3-й:
0 5 17 7
0 -5 -17 -7
0 5 17 7
3 -1 2 1
7 -4 -1 2
Умножим 4-ю строку на (7). Умножим 5-ю строку на (-3). Добавим 5-ю строку к 4-й:
0 5 17 7
0 -5 -17 -7
0 5 17 7
0 5 17 13
7 -4 -1 -2
Добавим 2-ю строку к 1-й:
0 0 0 0
0 -5 -17 -7
0 5 17 7
0 5 17 13
7 -4 -1 -2
Добавим 3-ю строку к 2-й:
0 0 0 0
0 0 0 0
0 5 17 7
0 5 17 13
7 -4 -1 -2
Умножим 4-ю строку на (-1). Добавим 4-ю строку к 3-й:
0 0 0 0
0 0 0 0
0 0 0 -6
0 5 17 13
7 -4 -1 -2
Для удобства вычислений поменяем строки местами:
0 0 0 0
0 0 0 0
0 0 0 -6
0 5 17 13
7 -4 -1 -2
Система не совместна. Так как при любых вычислениях в каждой строчке почти есть по нулю.
n)
Запишем систему в виде расширенной матрицы:
3 1 -1 -5 1
1 -4 3 -2 0
Умножим 2-ю строку на (-3). Добавим 2-ю строку к 1-й:
0 13 -10 1 1
1 -4 3 -2 0
Теперь исходную систему можно записать так:
Необходимо переменные x3,x4 принять в качестве свободных переменных и через них выразить остальные переменные.
Приравняем переменные x3,x4 к 0
Из 1-й строки выражаем x
Из 2-й строки выражаем x1