Предмет: Алгебра,
автор: twentyonepeople08
ПОМОГИТЕ, ПОЖАЛУЙСТА
Приложения:
Ответы
Автор ответа:
1
Объяснение:
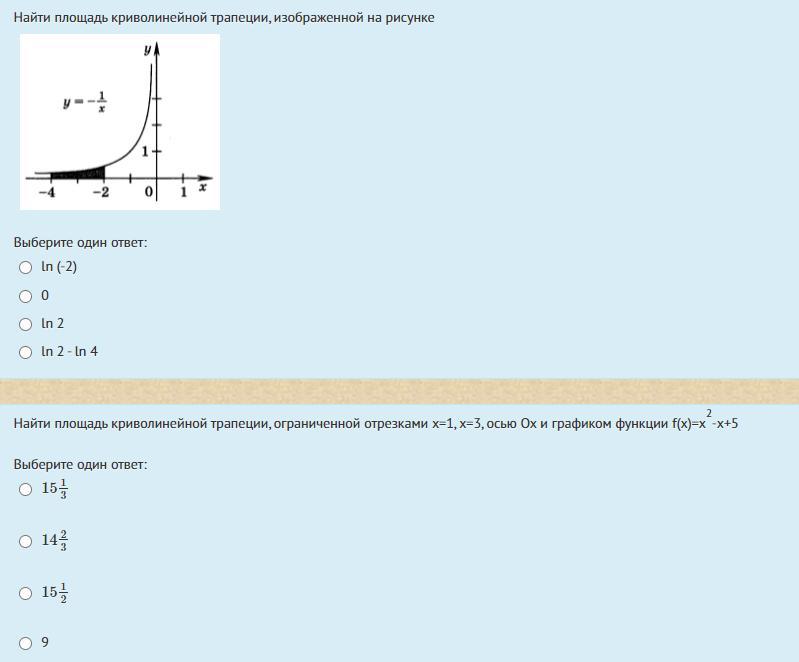
1) Площадь криволинейной трапеции есть определенный интеграл Римана на заданном промежутке.
Ответ: ln2 (3й вариант ответа)
2) То же самое, что и в 1, только функция другая и промежутки другие:
Для начала найдем значение неопределенного интеграла:
Теперь посчитаем значение определенного интеграла, восстановив промежутки интегрирования:
Ответ: (2й вариант ответа)
twentyonepeople08:
спасибо большое!!!
Похожие вопросы
Предмет: Русский язык,
автор: Елена1121
Предмет: Русский язык,
автор: Аноним
Предмет: Другие предметы,
автор: джеси25
Предмет: Русский язык,
автор: beja7
Предмет: Алгебра,
автор: kostruleva1985