!?Алгебра 9 класс
Срочно нужна ваша помощь
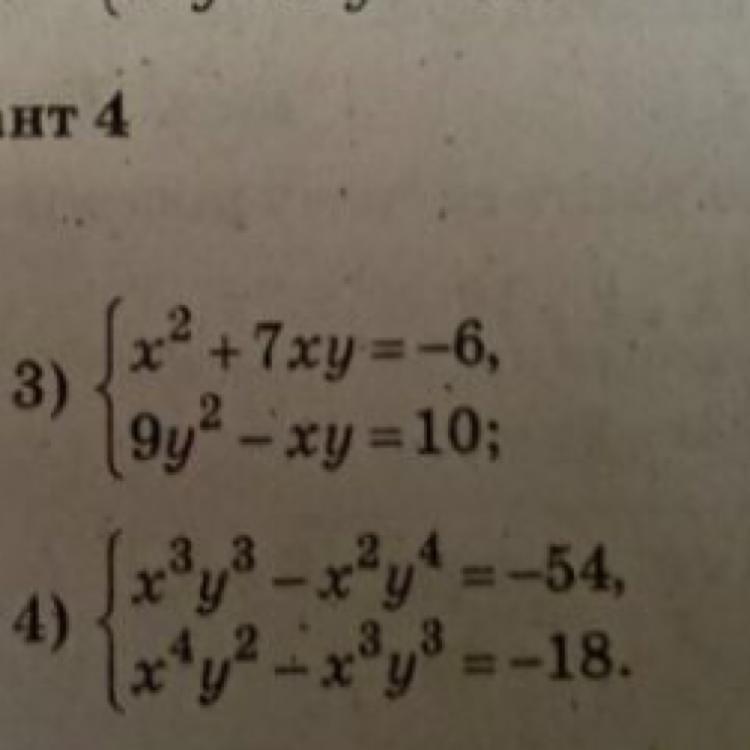
Ответы
Ответ:
3) y = -1; ; 1
4) Нет корней
Объяснение:
3) Прибавим левые и правые части уравнений системы:
+ 7xy + 9
- xy = 10 - 6
+ 6xy + 9
= 4
= 4
x + 3y = 2 x + 3y = -2
1) x = 2 - 3y 2) x = -3y - 2
По очереди подставим получившиеся значения х во второе уравнение:
1) 9 - (2 - 3y)y = 10
9 - 2y + 3
= 10
12 - 2y - 10 = 0
6 - y - 5 = 0
Решим через дискриминант:
a = 6 b = -1 c = -5
D = - 4ac = 1 + 120 = 121 =
=
=
= 1
=
=
=
2) 9 - (- 3y - 2)y = 10
9 + (3y + 2)y = 10
9 + 2y + 3
= 10
12 + 2y - 10 = 0
6 + y - 5 = 0
Решим через дискриминант:
a = 6 b = 1 c = -5
D = - 4ac = 1 + 120 = 121 =
=
=
=
=
=
= -1
Корень повторяется, а значит мы получили 3 различных корня:
y = -1; ; 1
4)
-
= -54
= -18
(x - y) = -54
(x - y) = -18 => 3
(x - y) = -54
=
3 =
Следовательно:
= 3
3 = 0
ОДЗ: х≠0, у≠0
= 0
= 0
х = 0
Противоречие ОДЗ, значит система корней не имеет.