Question

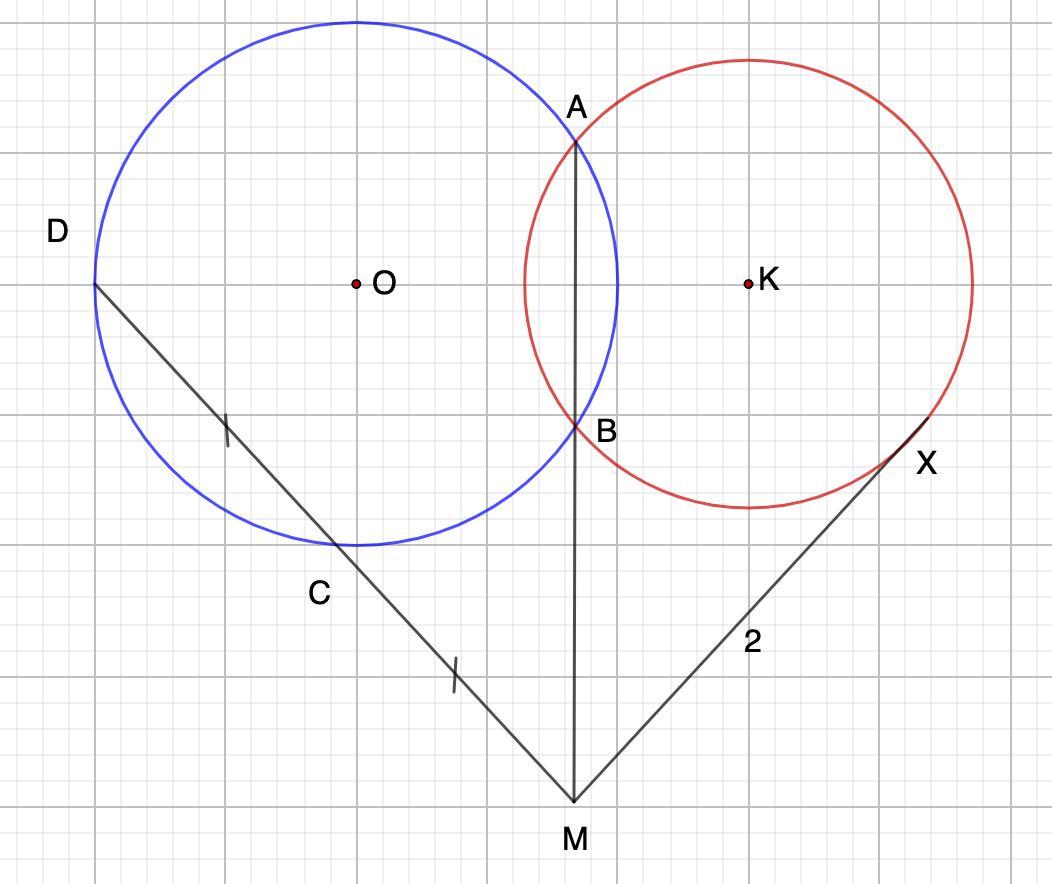
15 баллов, хелп ми, пожалуйста. Две окружности пересекаются в точках А и В. Из точки М на прямой АВ проведена секущая МСД к первой окружности и касательная МХ длины 2 ко второй.
Найдите СД, если известно, что С-середина МД.

Answer 1

Ответ:

Отрезок секущей СD равен √2 (ед).

Пошаговое объяснение:

Требуется найти отрезок секущей CD.

Дано: Окр.О ∩ Окр.К в точках А и В.

МСD - секущая;

МХ = 2 - касательная;

МС = CD.

Найти: CD.

Решение:

1. Рассмотрим Окр.К

МХ - касательная;

МВА - секущая.

• Свойство касательной и секущей: если из одной точки к окружности проведены касательная и секущая, то квадрат отрезка касательной равен произведению отрезка секущей и ее внешней части.

То есть:

МХ² = МВ · МА

Подставим значения МХ = 2 :

4 = МВ · МА

2. Рассмотрим Окр.О.

МВА - секущая;

СDX - секущая.

• Свойство двух секущих: Если из точки, лежащей вне окружности, проведены две секущие, то произведение одной секущей на ее внешнюю часть равно произведению другой секущей на ее внешнюю часть.

МА · МВ = MD · MC

MA · MB = 4 (п.1)

⇒ MD · MC = 4         (1)

3. МС = CD (по условию)

⇒ MD = 2CD

Заменим в выражении (1) MD на 2CD;   MC на CD и получим равенство:

2CD · CD = 4

CD² = 2

CD = √2 (ед)

Отрезок секущей СD равен √2 (ед).