Предмет: Математика,
автор: anton2992m
СРОЧНО ПОМОГИТЕ!
надо пипец как срочно!!!!!!!
Приложения:
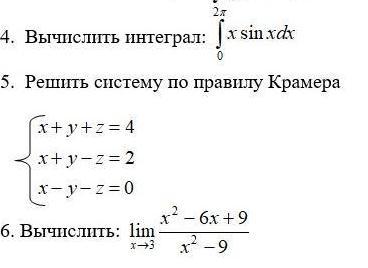
anton2992m:
с пояснением хорошо бы
Ответы
Автор ответа:
1
Ответ:
Интегрирование по частям .
Метод Крамера решения СЛУ .
Неопределённость вида
Похожие вопросы
Предмет: Русский язык,
автор: памойму1939
Предмет: Русский язык,
автор: Болган
Предмет: Русский язык,
автор: JULIA1234558798UY
Предмет: Английский язык,
автор: Loveyouannyar
Предмет: Химия,
автор: hjvghggyfsff