Предмет: Алгебра,
автор: anik200579
алгебра номер 17.5(3) помогите пожалуйста
Приложения:
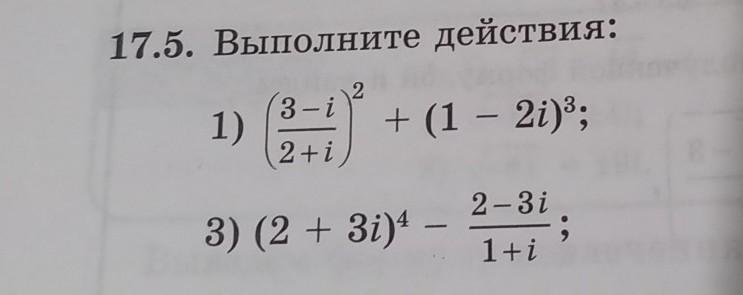
Ответы
Автор ответа:
2
Ответ:
eugeniodepez:
Здравствуйте,помогите решить задание по алгебре даю 50 баллов на ответ)
Похожие вопросы
Предмет: Русский язык,
автор: samoylova1331
Предмет: Русский язык,
автор: 1eet2
Предмет: Русский язык,
автор: bru79
Предмет: Русский язык,
автор: bykov4natasha