Предмет: Алгебра,
автор: carlidamelio290
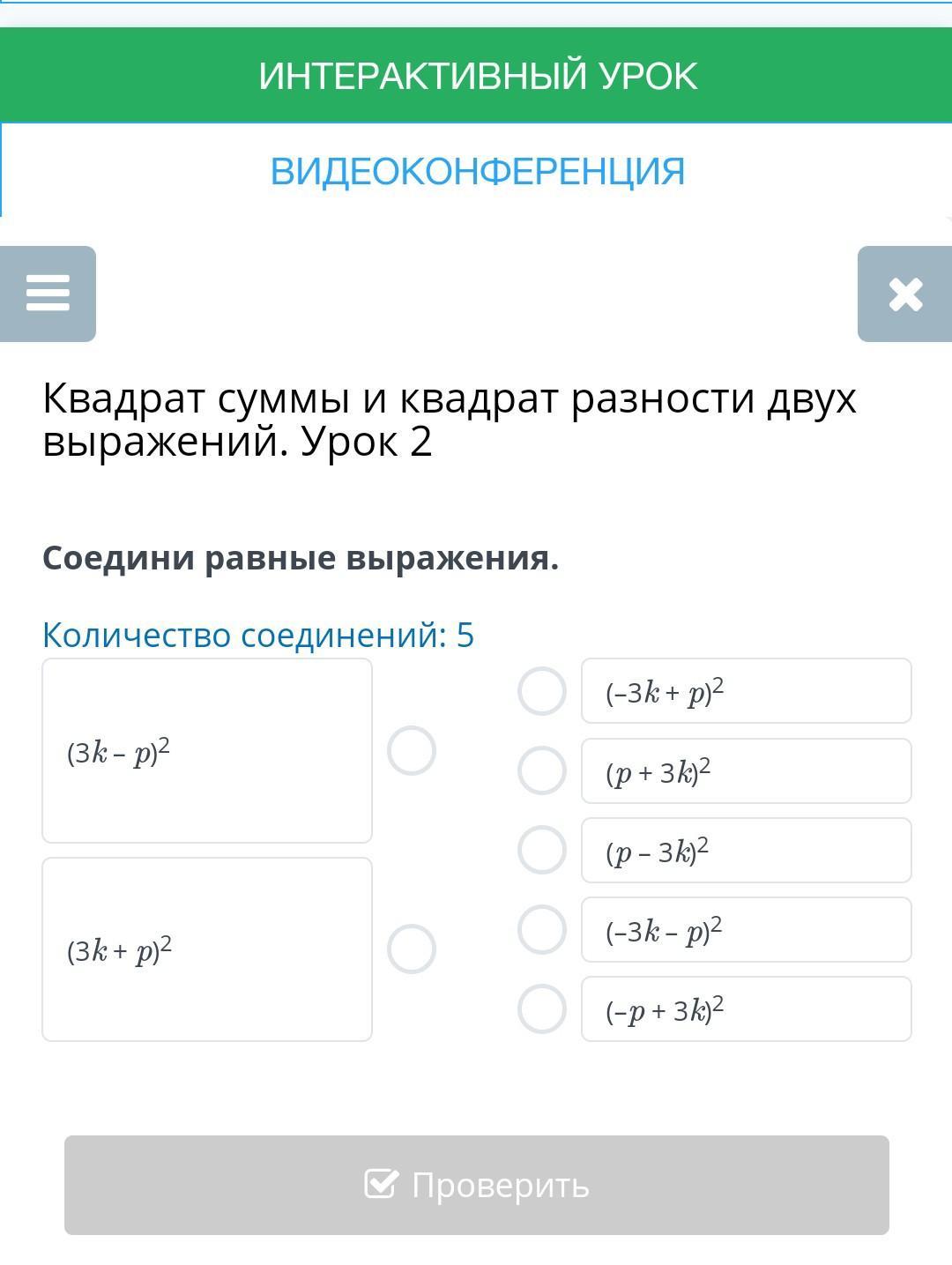
ПОМОГИТЕ ДАМ 10 БАЛЛОВ!!!Квадрат суммы и квадрат разности двух выражений. Урок 2 Соедини равные выражения. Количество соединений: 5 (-3k + p)² (3k-p)² (p+ 3k)² k+ p)² Проверить (p-3k)² (-3k-p)² (-p+ 3k)²
Приложения:
Ответы
Автор ответа:
48
Ответ:
(3k - p)² = (-3k + p)² = (p - 3k)² = (-p + 3k)²
(3k + p)² = (p + 3k)² = (-3k - p)²
Объяснение:
Воспользуемся определением степени (), правилами раскрытия скобок и законами сложения для преобразования выражений в правой части к одному из выражений в левой части
, поскольку
по переместительному закону сложения
, поскольку
по переместительному закону сложения
seregamelnik092:
боже мой спасите какой ответ
короч кто не пон
3k - p)² = (-3k + p)² = (p - 3k)² = (-p + 3k)²
(3k + p)² = (p + 3k)² = (-3k - p)²
(3k + p)² = (p + 3k)² = (-3k - p)²
спасибо большое
спасибо
блин не чё не понел скажите 1 туда туда 2 тож также также лехче
пожалуйста
итоговый ответ в самом начале
спасибо
Спасибо не правильно
Похожие вопросы
Предмет: Английский язык,
автор: irenka0bakaJuLiana
Предмет: Английский язык,
автор: marynialera
Предмет: Қазақ тiлi,
автор: basarbaevaainu
Предмет: Литература,
автор: sr5sd8
Предмет: Математика,
автор: Vingo241