Question

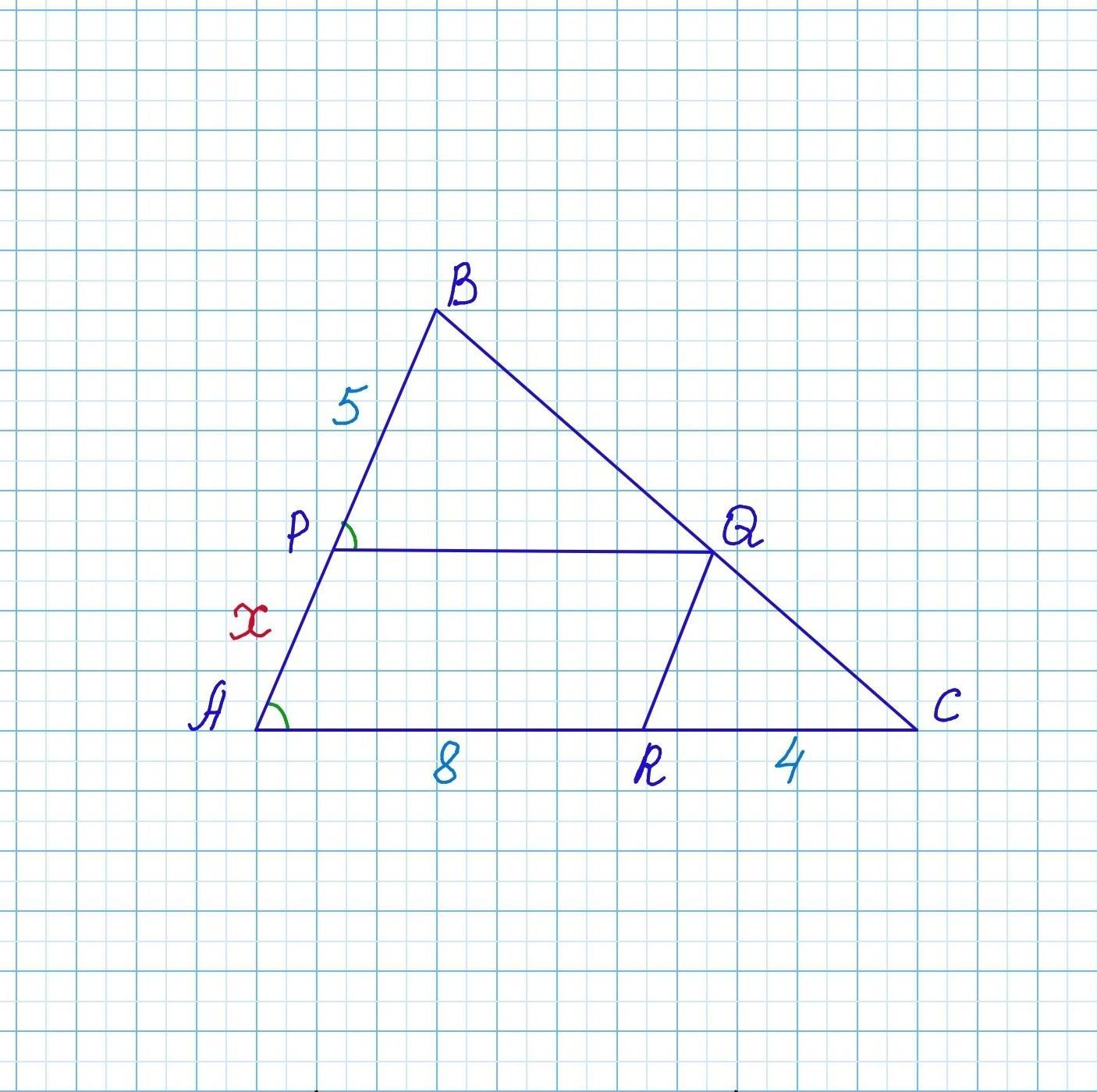
На сторонах AB, BC и CA треугольника ABC выбраны точки P, Q и R соответственно таким образом, что PQ ∥ AC, а QR ∥ AB. Найдите отрезок AP, если BP = 5, AR = 8, RC = 4.

Answer 1

Ответ:

2,5 ед

Объяснение:

Так как PQ ∥ AC, а QR ∥ AB, то APQR - параллелограмм.

• Параллелограмм это четырехугольник у которого противоположные стороны попарно параллельны

Так как в параллелограмме противоположные стороны равны то PQ=AR=8 ед.

Рассмотрим △АВС и △PBQ.

∠BAC =∠BPQ - как соответственные углы при параллельных прямых PQ и AC и секущей АВ.

∠B - общий.

Следовательно △АВС подобен △PBQ.

Из подобия треугольников следует пропорциональность соответственных сторон:

$\dfrac{AB}{PB} = \dfrac{AC}{PQ} \\ \\ \dfrac{x + 5}{5} = \dfrac{12}{8} \\ \\ 8(x + 5) = 12 \times 5 \\ \\ 8x = 60 - 40 \\ \\ x = \frac{20}{8} = 2.5$

АР = 2,5 ед