Предмет: Алгебра,
автор: milaantonova910
Решите систему уравнений
Приложения:
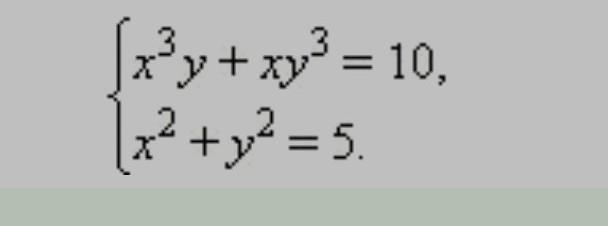
Ответы
Автор ответа:
1
Объяснение:
Ответ: (1;2) (2;1) (-2;-1) (-1;-2).
milaantonova910:
Большое спасибо ❤️
Здравствуйте, помогите пожалуйста решить теория вероятности
уважаемый sangers 1959 вы здесь
Похожие вопросы
Предмет: Русский язык,
автор: cat25251
Предмет: Русский язык,
автор: AnyPozitivchik
Предмет: Немецкий язык,
автор: krivopuskanna1
Предмет: Другие предметы,
автор: Аноним