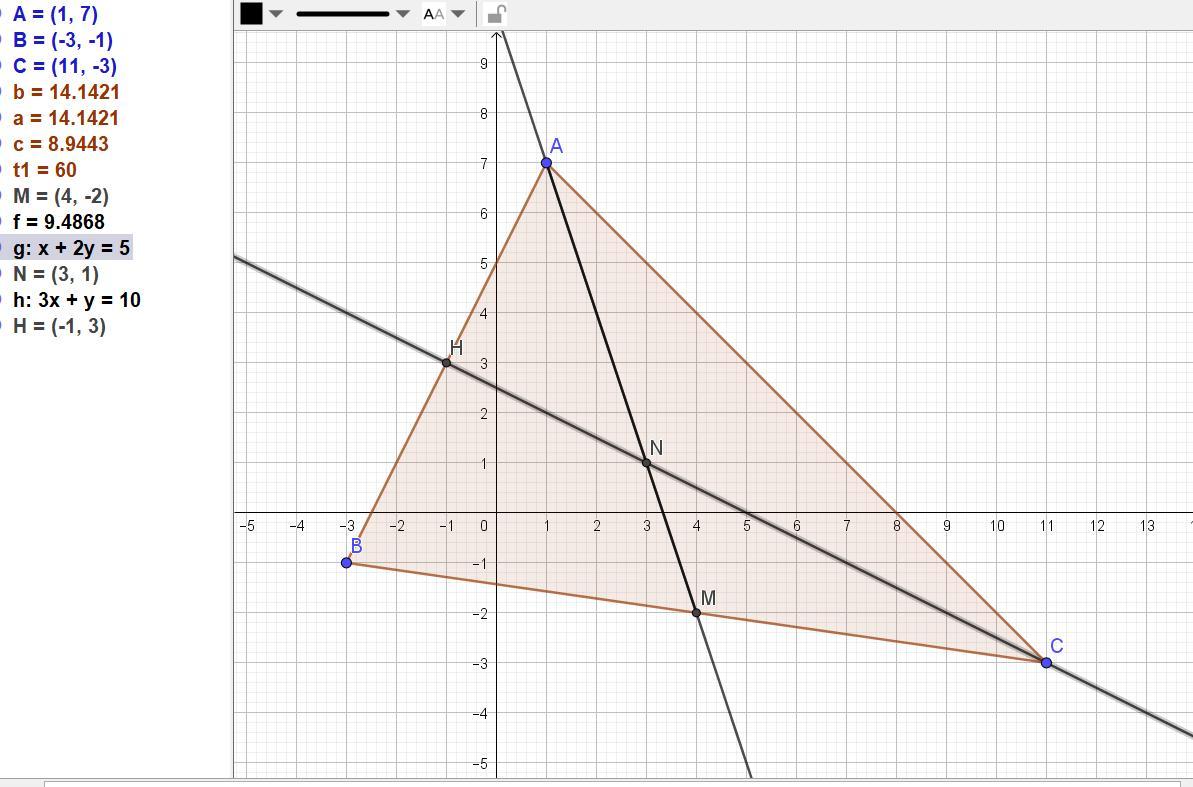
Даны вершины треугольника ABC:A(x1;y1), B(x2;y2), C(x3;y3)
Найти
а) уравнение стороны АВ
б) уравнение высоты АВ
с) уравнение медианы АМ
г) точку N пересечения медианы AM и высоты CH
д) уравнение прямой, проходящей через вершину С параллельно стороне AB
При A(1;7) B(-3;-1) C(11;-3)
Ответы
Даны вершины треугольника ABC: A(1;7) B(-3;-1) C(11;-3)
Найти
а) уравнение стороны АВ.
Находим вектор АВ = (-3-1; -1-7) = (-4; -8).
Уравнение АВ: (x – 1)/(-4) = (y – 7)/(-8) или 2x – y + 5 = 0 в общем виде.
б) уравнение высоты АD.
Находим уравнение стороны ВС.
Вектор ВС = (11-(-3); -3-(-1)) = (14; -2)
Уравнение ВС: (x + 3)/14 = (y + 1)/(-2) или в общем виде x + 7y + 10 = 0.
У перпендикулярной прямой к прямой в общем виде Ах + Ву + С = 0 коэффициенты переменных А и В меняются на В и (-А) (чтобы их скалярное произведение равнялось нулю).
Тогда уравнение AD: 7x – y + C = 0. Для определения слагаемого С подставим координаты точки А: 7*1 – 7 + С = 0, отсюда С = 7 – 7 = 0.
Уравнение AD: 7x – y = 0.
с) уравнение медианы АМ.
Находим координаты точки М как середины стороны ВС.
М = (B(-3;-1) + C(11;-3))/2 = (4; -2).
Вектор АМ = (4-1; -2-7) = (3; -9).
Уравнение медианы АМ: (x – 1)/3 = (y – 7)/(-9) или в общем виде 3x + y – 10 = 0.
г) точку N пересечения медианы AM и высоты CH.
Прямая СН – это перпендикуляр к АВ: 2x – y + 5 = 0.
Уравнение СН: x + 2y + C = 0. Подставим С = (11; -3).
11 + 2*(-3) + С = 0, отсюда С = -11 + 6 = -5.
Уравнение СН: x + 2y - 5 = 0.
Находим точку пересечения АМ и СН.
АМ: 3x + y – 10 = 0. (х(-2)) = -6х – 2у + 20 = 0
СН: x + 2y - 5 = 0. x + 2y - 5 = 0
-5х + 15 = 0,
х = -15/(-5) = 3, у = 10 – 3х = 10 – 3*3 = 1.
Точка N(3; 1).
д) уравнение прямой, проходящей через вершину С параллельно стороне AB.
У этой прямой коэффициенты при переменных сохраняются.
2x – y + С = 0, подставим С = (11; -3).
2*11 – (-3) + С = 0, отсюда С = -22 – 3 = -24.
Уравнение: 2x – y - 24 = 0.