Предмет: Математика,
автор: Hn94
Вища математика.
Розв'язати
Приложения:
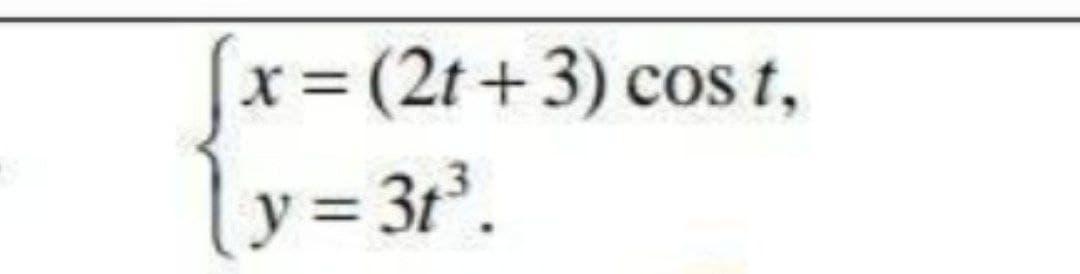
TheTedra:
что мне с этим сделать? Не знаю украинского
а что здесь. найти производную?
да
Ответы
Автор ответа:
2
Находим производные от х и от у по параметру t.
dy/dt=9t²
dx/dt=(2t+3)'*cost+(cost)'*(2t+3)=2*cost-sint*(2t+3)
dy/dx=(dy/dt): (dx/dt)=(9t²/(2*cost-sint*(2t+3))
Спасибо, очень помог
Автор ответа:
2
Ответ:
Похожие вопросы
Предмет: Английский язык,
автор: геля135
Предмет: Українська мова,
автор: DaKrulzz
Предмет: Русский язык,
автор: Sharenkina
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: alexkovarnii72