Найти абсциссу точки
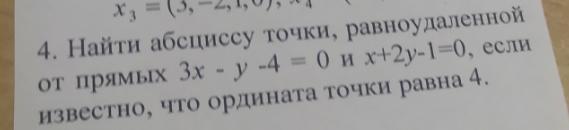
Ответы
Так как заданные прямые, пересекаясь, образуют 2 пары углов, то задача имеет 2 решения – искомая точка имеется как на биссектрисе одно угла, так и на биссектрисе второго угла.
Пусть точка H(х;у) лежит на биссектрисе угла между прямыми.
Это значит, что расстояние d1 это точки до прямой l1 равно
расстоянию d2 это точки до прямой l2.
Используем формулу расстояния от точки до прямой.
d1=|3x–y-4|/√(3²+(-1)²),
d2=|x+2y-1|/√(1²+2²),
d1=d2 ⇒ |3x–y-4|/√(3²+(-1)²) =|x+2y-1|/√(1²+2²) .
Раскрывая модуль и подставив вместо «у» заданное значение 4, получаем 2 решения:
(3x–4-4)/√(3²+(-1)²) = (x+2*4-1)/√(1²+2²)
(3x–8)/√10 = (x+7)/√5.
Умножаем числитель и знаменатель правой части на √2 и приравниваем числители обеих частей.
(3x–8) = (x+7)*√2.
x(3 - √2) = 8 + 7√2.
х = (8 + 7√2)/( 3 - √2) ≈ 11,28746.
Аналогично находим второе решение, раскрыв модуль с другим знаком.
(3x–4-4)/√(3²+(-1)²) = -(x+2*4-1)/√(1²+2²)
(3x–8)/√10 = -(x+7)/√5.
Умножаем числитель и знаменатель правой части на √2 и приравниваем числители обеих частей.
(3x–8) = -(x+7)*√2.
x(3 + √2) = 8 - 7√2.
х = (8 - 7√2)/( 3 + √2) ≈ -0,43031.
Ответ: абсциссы заданных точек имеют значения
х = (8 + 7√2)/( 3 - √2) ≈ 11,28746.
х = (8 - 7√2)/( 3 + √2) ≈ -0,43031.
