Предмет: Алгебра,
автор: kopotvrot
решите систему уравнений
Приложения:
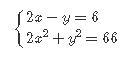
Ответы
Автор ответа:
1
Відповідь:
решение на фотографии...
Приложения:
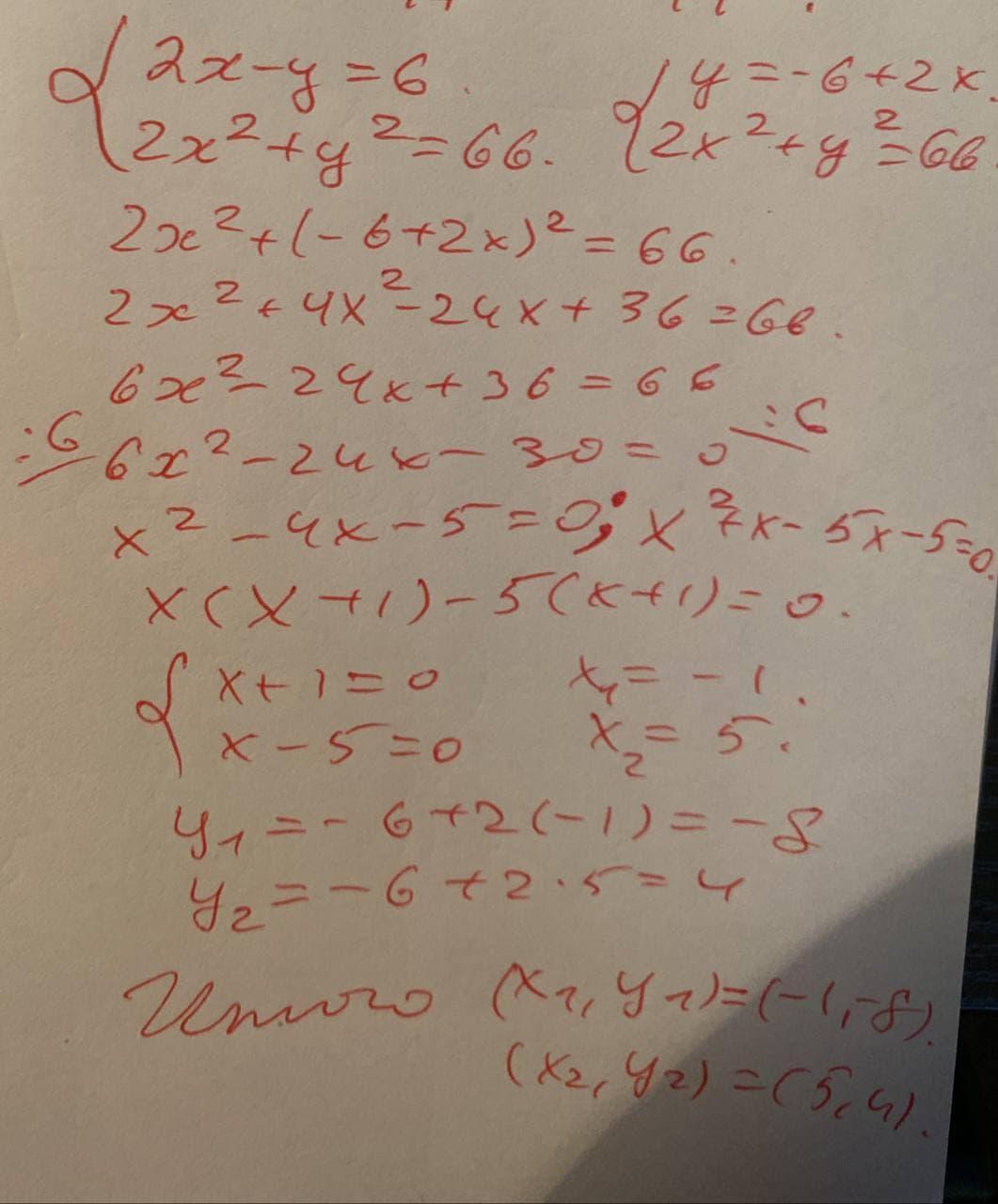
Автор ответа:
1
методом подстановки заменили переменную y² и получили уравнение с одной переменной
2х²+(2х-6)²=66
раскрываем скобки формулой сокращенного умножения (a-b)²=a²-2ab+b²
2x²+(2x)²-2×6×2x+6²=66
2x²+4x²-24x+36-66=0
6x²-24x-30=0
уравнение типа ax²+bx+c=0
по одной теореме если a-b+c=0 то х₁=-1 х₂=-с/а
a-b+c=6-(-24)+(-30)=6+24-30=0 ⇒ x₁=-1 х₂=с/а=-(-30)/6=30/6=5
подставляем y₁=2×(-1)-6=-8 y₂=2×5-6=4
Ответ: (-1;-8) и (5;4)
Похожие вопросы
Предмет: Английский язык,
автор: AigulLife
Предмет: Английский язык,
автор: iNS1Die
Предмет: Русский язык,
автор: 23KIRIL08
Предмет: Английский язык,
автор: alinlobova
Предмет: География,
автор: RyaBchicK