Предмет: Геометрия,
автор: abramyan0707
Дан треугольник АВС. Если АВ=15 см, ВС=14 см, угол В=60 градусов, то найди длинну стороны АС. СРОЧНО НУЖНО, ПОЖАЛУЙСТА!
Ответы
Автор ответа:
3
Ответ:
Длина стороны см.
Объяснение:
Наша задача найти неизвестную сторону треугольника по двум известным сторонам и углу между ними.
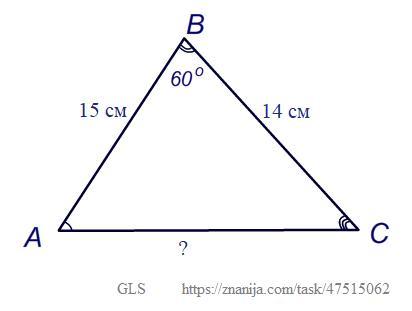
Дано: ΔABC, AB = 15 см, BC = 14 см, ∠B = 60°.
Найти: AC.
Решение.
Решим задачу по теореме косинусов: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.
(см).
Длина стороны см.
Приложения:
Автор ответа:
2
Ответ:
Длина стороны АС =√211 см = 14,5 см.
Объяснение:
Требуется найти сторону АС.
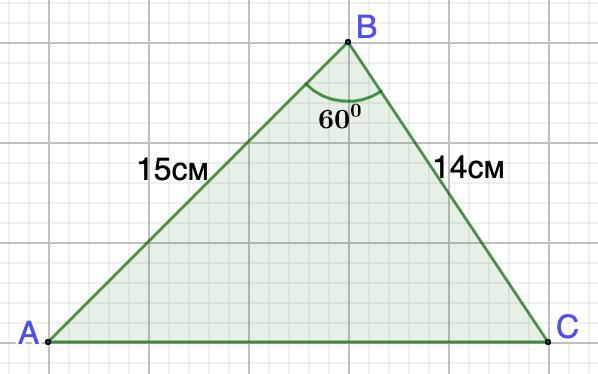
Дано: ΔАВС;
АВ = 15 см; ВС = 14 см;
∠В = 60°.
Найти: АС.
Решение:
Чтобы найти сторону АС, воспользуемся теоремой косинусов:
- Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
Применим теорему косинусов для нашей задачи:
Подставим данные значения и найдем АС:
⇒ Искомая сторона АС = √211 см = 14,5 см.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Vanyadog
Предмет: Технология,
автор: nastiamitina30
Предмет: Русский язык,
автор: НастяФейгус
Предмет: Алгебра,
автор: errdygftyyffyh
Предмет: Английский язык,
автор: ivan034