Question

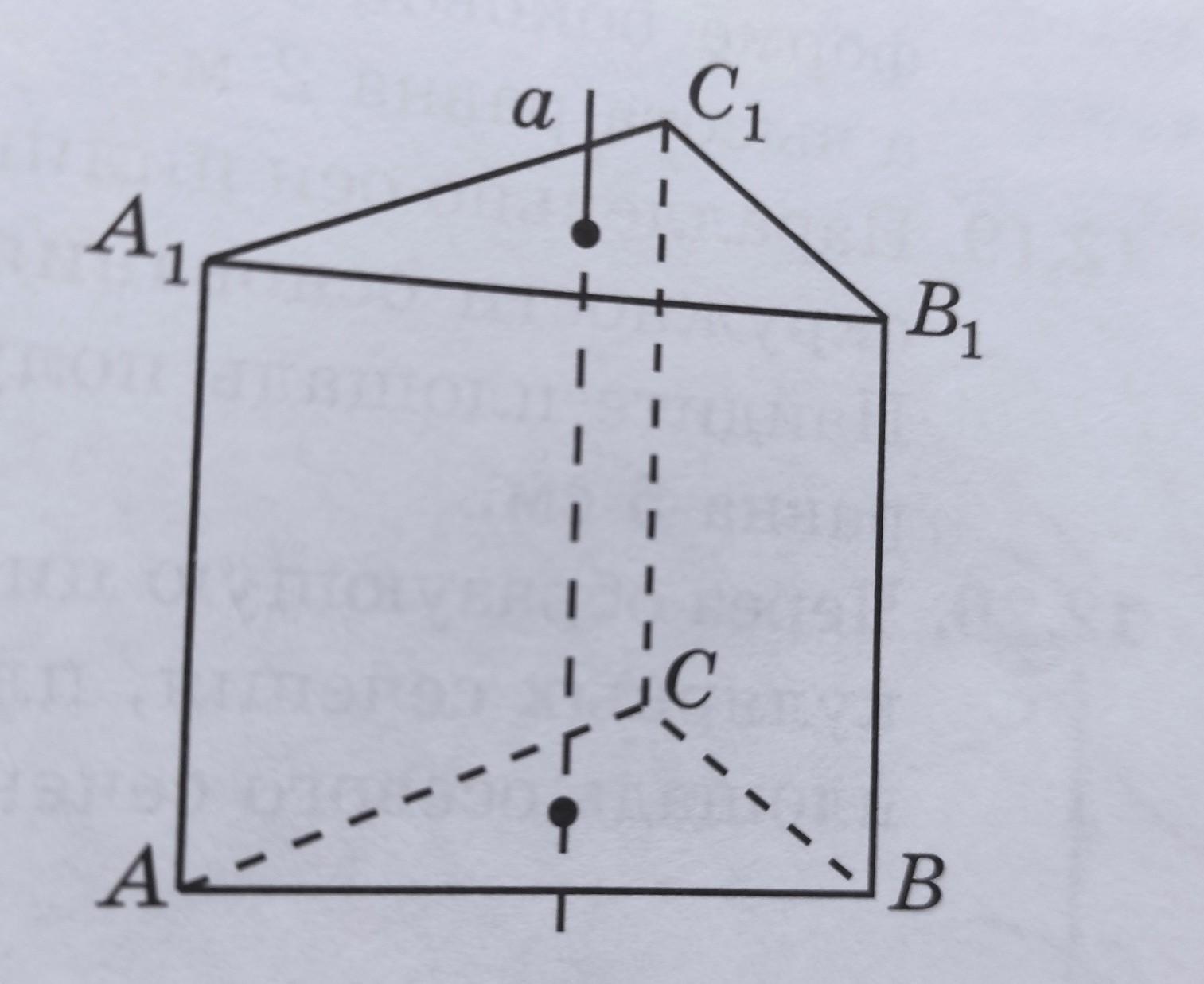
найдите площадь боковой поверхности цилиндра, получающегося вращением правильной треугольной призмы, все ребра которой равны 1 см, вокруг прямой:
а) содержащей боковое ребро
б)проходящей через центры ее основании​

Answer 1

Ответ:

а) 2π см²

б) π√3 см²

Объяснение:

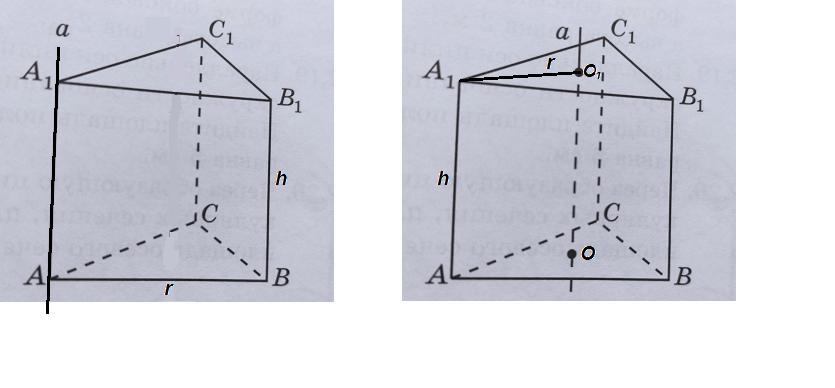
а) Если призма вращается вокруг прямой, содержащей боковое ребро, то в полученном цилиндре радиус основания равен ребру основания призмы, а высота равна длине бокового ребра:

r = AB = 1 см

h = BB₁ = 1 см

Площадь боковой поверхности цилиндра:

$S=2\pi rh$

$S=2\cdot \pi \cdot 1\cdot 1=2\pi$ см²

б) Если призма вращается вокруг прямой, проходящей через центры ее оснований, то в полученном цилиндре радиус основания равен радиусу окружности, описанной около основания призмы, а высота равна длине бокового ребра:

$r=O_1A_1=\dfrac{AB\sqrt{3}}{2}=\dfrac{\sqrt{3}}{2}$  см

h = BB₁ = 1 см

Площадь боковой поверхности цилиндра:

$S=2\pi rh$

$S=2\cdot \pi \cdot \dfrac{\sqrt{3}}{2}\cdot 1=\pi \sqrt{3}$  см²