Question

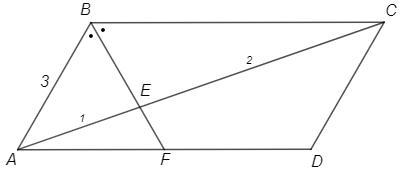
В параллелограмме ABCD сторона AB=3м, а угол B=120°. Биссектриса угла B делит диагональ AC в отношении 2:1, считая от вершины C. Найдите площадь параллелограмма ABCD.

Answer 1

Углы A и B параллелограмма - внутренние односторонние при параллельных, сумма 180.

∠BAD=180-∠ABC =180-120 =60°

∠ABF =B/2 =120/2 =60° (BF - биссектриса)

△ABF - равносторонний (т.к. два угла 60°) => AF=AB=3

△BEC~△FEA (по накрест лежащим при AD||BC)

=> BC/AF=CE/AE=2/1 => BC=2AF=6

S(ABCD) =AB*BC*sin(ABC) =3*6*sin120 =9√3 (м^2)