Предмет: Математика,
автор: milkspi
ПОМОГИТЕ ПОЖАЛУЙСТА ЭТО ООЧЕНЬ ВАЖНО....
Приложения:
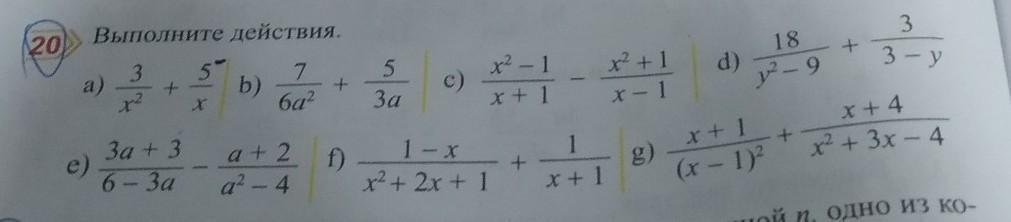
Ответы
Автор ответа:
1
а)
b)
c)
d)
e)
f)
g)
milkspi:
Как и всегда большое спасибо)
Похожие вопросы
Предмет: Русский язык,
автор: shishovaulya
Предмет: Русский язык,
автор: гуль12
Предмет: Русский язык,
автор: eefimova1977
Предмет: Русский язык,
автор: nikitasem14
Предмет: Английский язык,
автор: nosocheksosochek