Question

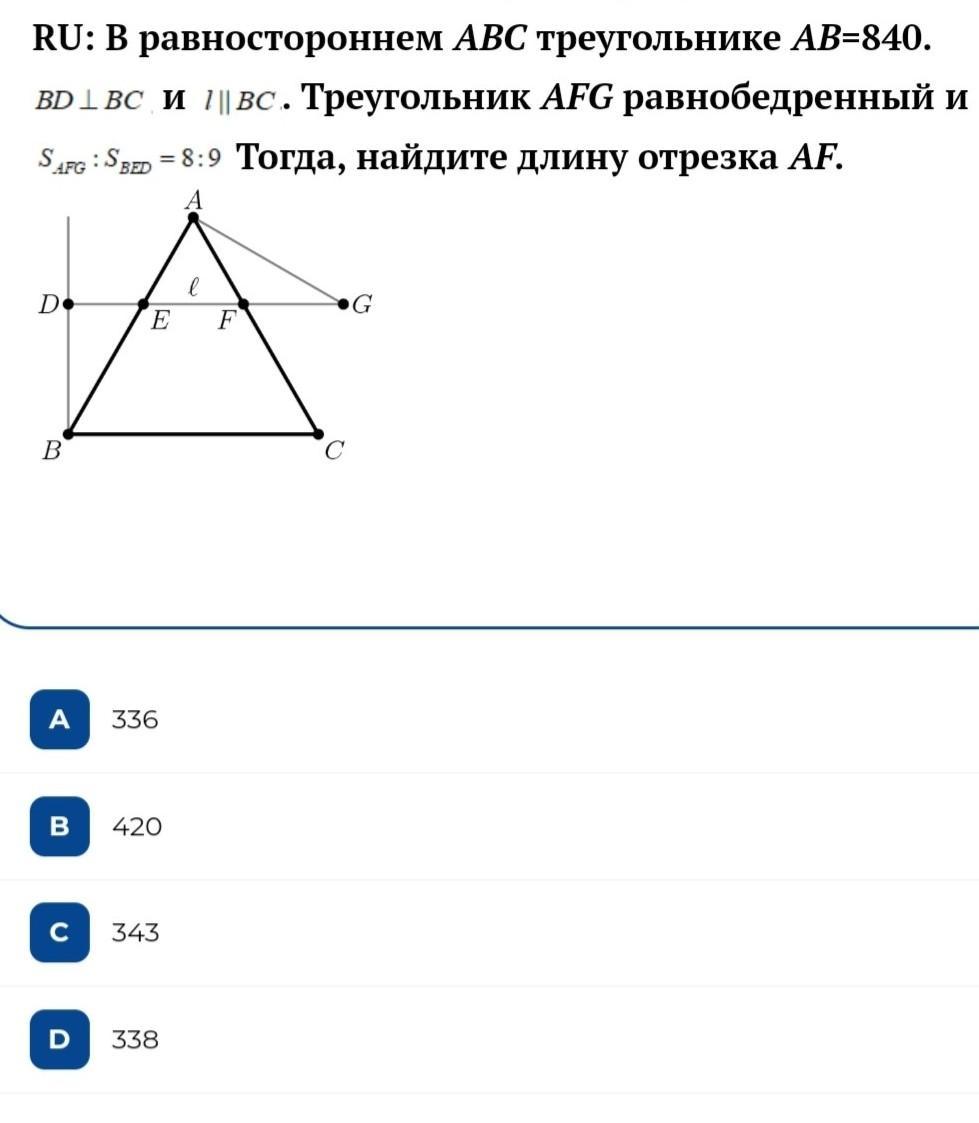
математика задача №17​

Answer 1

Ответ:

336

Пошаговое объяснение:

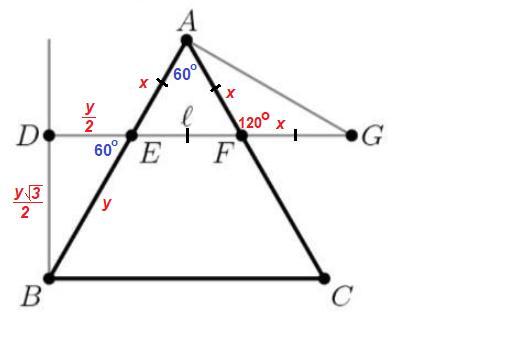
• Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.

ΔEAF ~ ΔBAC, тогда

ΔEAF тоже правильный, все углы по 60°.

EF = AE = AF = FG = x

Обозначим ВЕ = у.

AE + BE = AB

x + y = 840           (1)

∠DEB = ∠AEF = 60° как вертикальные,

∠BDE = 90°,  ⇒  ∠DBE = 30°, катет, лежащий против этого угла в треугольнике BDE, равен половине гипотенузы:

DE = 0,5 BE = y/2

По теореме Пифагора:

$BD=\sqrt{BE^2-DE^2}=\sqrt{y^2-\dfrac{y^2}{4}}=\dfrac{y\sqrt{3}}{2}$

Площадь треугольника AFG:

$S_{AFG}=\dfrac{1}{2}AF\cdot FG\cdot \sin\angle AFG$

∠AFG = 180° - ∠AFE = 180° - 60° = 120°

$\boldsymbol{S_{AFG}}=\dfrac{1}{2}\cdot x\cdot x\cdot \dfrac{\sqrt{3}}{2}\boldsymbol{=\dfrac{x^2\sqrt{3}}{4}}$

Площадь прямоугольного треугольника  BDE:

$\boldsymbol{S_{BDE}}=\dfrac{1}{2}BD\cdot DE=\dfrac{1}{2}\cdot \dfrac{y\sqrt{3}}{2}\cdot \dfrac{y}{2}\boldsymbol{=\dfrac{y^2\sqrt{3}}{8}}$

Отношение площадей дано:

$\dfrac{x^2\sqrt{3}}{4}:\dfrac{y^2\sqrt{3}}{8}=\dfrac{8}{9}$

$\dfrac{x^2\sqrt{3}}{4}\cdot \dfrac{8}{y^2\sqrt{3}}=\dfrac{8}{9}$

$\dfrac{2x^2}{y^2}=\dfrac{8}{9}$

$9x^2=4y^2$

$3x=2y$     (так как х и у положительные)

$y=\dfrac{3}{2}x$

Подставим в уравнение (1):

$x+\dfrac{3}{2}x=840$

$2,5x=840$

x = 336

EF = 336

Answer 2

Відповідь:

Покрокове пояснення:

А) 336