Question

Решение текстовых задач с помощью составления дробно-рациональных уравнений. Урок 1

Два велосипедиста одновременно отправляются в 30-километровый заезд по национальному природному парку Бурабай. Первый едет со средней скоростью на 4 км/ч большей, чем второй, и прибывает к финишу на 2 ч раньше второго. Найди скорость велосипедиста, пришедшего к финишу вторым.

Ответ:км/

Answer 1

Ответ:

6 км/ч

Объяснение:

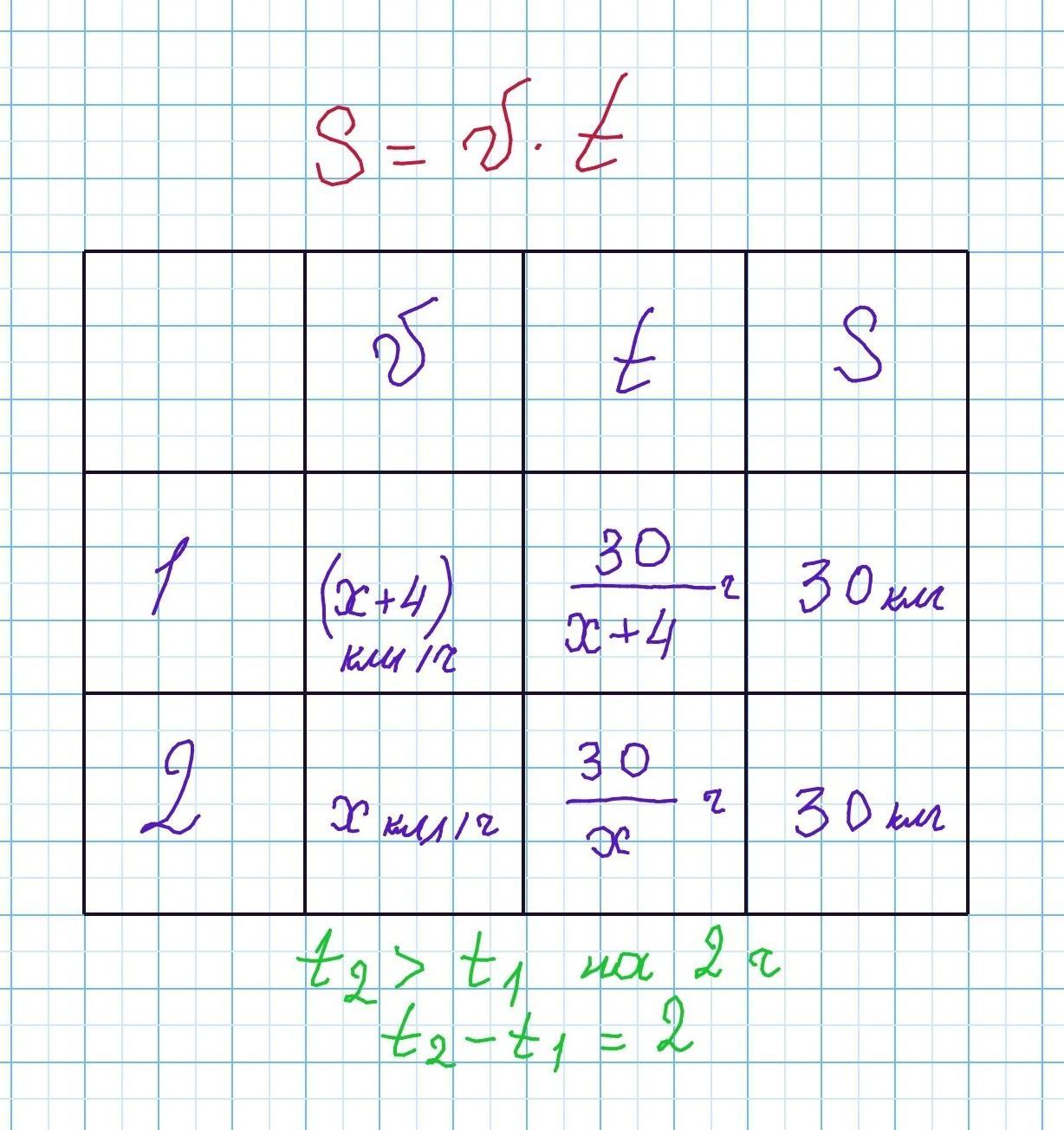
Пусть х км/ч - скорость второго велосипедиста,

(х + 4) км/ч - скорость первого.

Оба велосипедиста проехали по 30 км.

Запишем данные в таблицу, по строке выразим время движения каждого велосипедиста (расстояние разделить на скорость).

Время движения первого велосипедиста:

$\dfrac{30}{x+4}$  ч

Время движения второго велосипедиста:

$\dfrac{30}{x}$  ч

Известно, что первый велосипедист прибывает к финишу на 2 ч раньше второго, т.е. время движения у него меньше. Вычитаем из большего времени меньшее и получаем уравнение:

$\dfrac{30}{x}-\dfrac{30}{x+4}=2$

$\dfrac{30}{x}-\dfrac{30}{x+4}-2=0$

$\dfrac{30(x+4)-30x-2x(x+4)}{x(x+4)}=0$

x > 0 по смыслу задачи, поэтому умножаем на знаменатель обе части уравнения.

$30(x+4)-30x-2x(x+4)=0$

$30x+120-30x-2x^2-8x=0$

$2x^2+8x-120=0$

$x^2+4x-60=0$

По теореме, обратной теореме Виета,

$x_1=-10$ - не подходит по смыслу задачи,

$x_2=6$ (км/ч) - скорость второго велосипедиста.

Answer 2

Ответ:

6 км/ч

Объяснение:

Пусть скорость второго велосипедиста х км/ч, тогда скорость первого (х+4)км/ч. Второй велосипедист на путь в 30 км потратил 30/х ч, первый на то же расстояние потратил

$\dfrac{30}{x + 4}$ч

что на 2 часа меньше, чем потратил второй.

$\dfrac{30}{x} - \dfrac{30}{x + 4} = 2 \\ \\ \dfrac{30x + 120 - 30x}{x(x + 4)} = 2 \\ \\ \dfrac{120}{ {x}^{2} + 4x } = 2 \\ \\ 2 {x}^{2} + 8x - 120 = 0 \\ \\ {x }^{2} + 4x - 60 = 0 \\ \\ D = {b}^{2} - 4ac = 16 + 4 \times 60 = 256 = {16}^{2} \\ \\ x_1 = \dfrac{ - b + \sqrt{D} }{2a} = \dfrac{ - 4 + 16}{2} = 6 \\ \\ x_2 = \frac{ - b - \sqrt{D} }{2a} = \frac{ - 4 - 16}{2} < 0$

второй корень <0 не подходит при смыслу.

Поэтому скорость велосипедиста, пришедшего к финишу вторым равна 6 км/ч