Предмет: Алгебра,
автор: blindeye21
Запишите в виде многочлена стандартного вида выражение: 1) (х – 1)2 – х(х + 1)(х – 3); 2) (х – 1)х2 + 3(х – 3)2; 3; 3) (х – 2)2 +3(х + 1) - (х + 9); 4) (х – 3)(х + 1) + 2х(х2 - 2х). - -
Приложения:
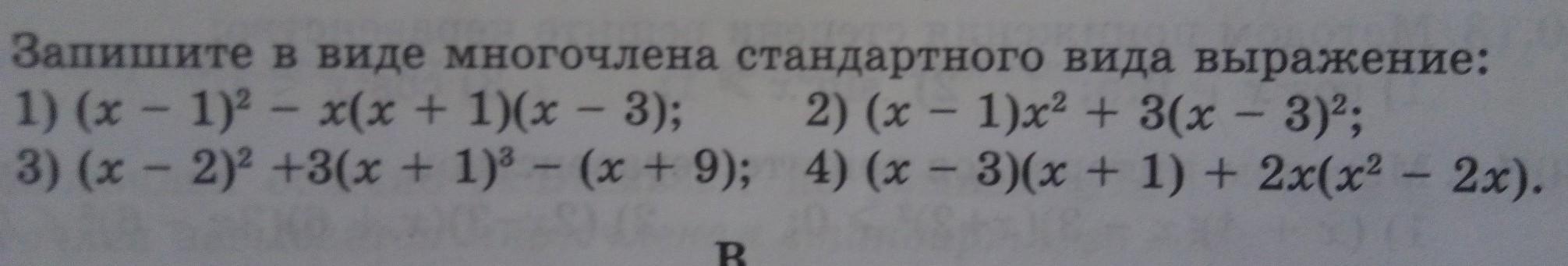
Ответы
Автор ответа:
0
Объяснение:
Раскроем скобки и приведем подобные слагаемые. Для этого применим формулы сокращенного умножения
и правилами умножения одночлена на многочлен и многочлена на многочлен.
Похожие вопросы
Предмет: Русский язык,
автор: Dianochka030711
Предмет: Українська мова,
автор: kosazcanata
Предмет: Русский язык,
автор: Autok2015
Предмет: Геометрия,
автор: vanabagrancev