Постройте график функции y=x^2 + 3 и опишите его свойства
Ответы
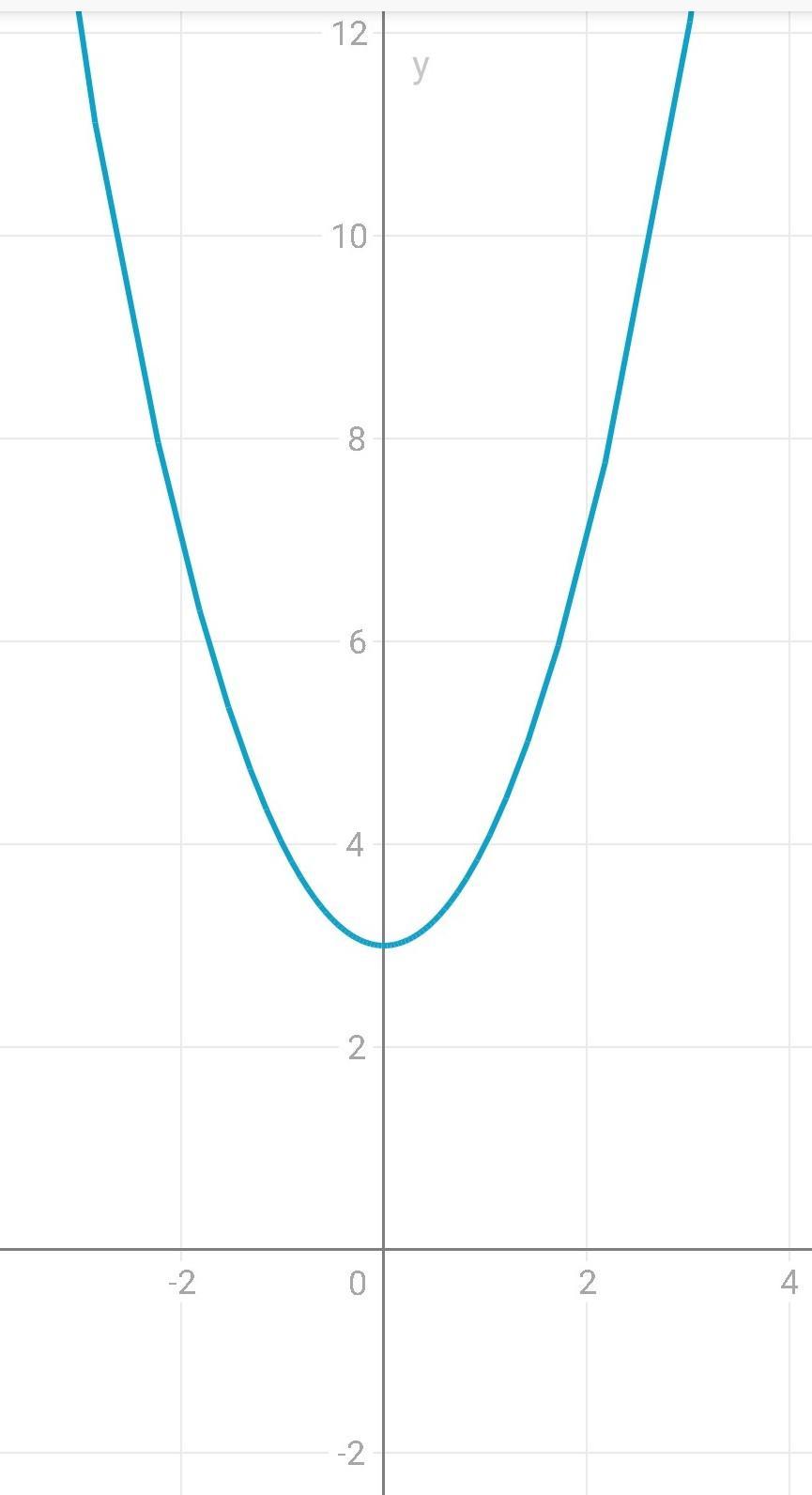
1. Область определения х∈(-∞;+∞)
2. Множество значений у∈[3;+∞)
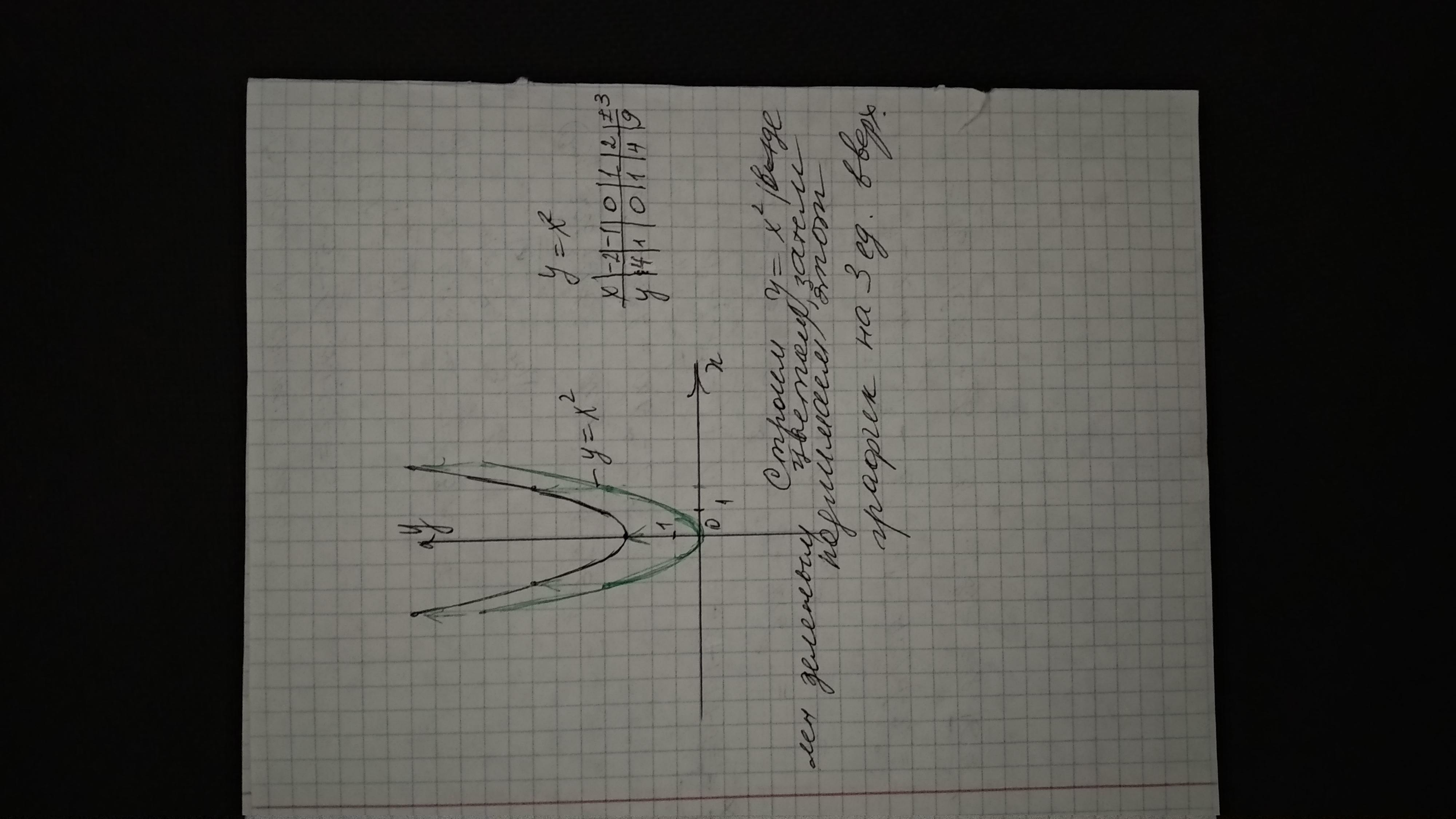
3. нулей нет. т.к. парабола у= х²поднята на 3 ед. вверх. ветви ее направлены вверх.
при любых значениях х у больше нуля.
4. функция возрастает при х∈[0;+∞) и убывает при х∈(-∞;0)
5. функция четна. т.к. ее график симметричен относительно оси оу.
6. ограничена снизу.
7. нет . не обратима. х²=у-3; х=±√(у-3), у=±√(х-3); но если рассматривать данную функцию только на множестве положительных чисел, она будет обратимой, а вообще обратимая - это функция, у которой произвольному ее значению соответствует единственное значение аргумента.
график во вложении
1) Область определения?
2) Множество значений?
3) нули функции?
4) На каких интервалах функция убывает и возрастает?
5) Функция четная или нет?
6) Ограничена?
7) Обратима или нет?
Ответ:
D-область определения по х
D є R
E-область значения по у
Е [3;+∞)
убывания и возрастание по х
↘(-∞;0]
↗[0;+∞)
min (0;3)
1) Область определения?
2) Множество значений?
3) нули функции?
4) На каких интервалах функция убывает и возрастает?
5) Функция четная или нет?
6) Ограничена?
7) Обратима или нет?