В правильной шестиугольной призме, все ребра которой равны 1, найдите угол между прямой AE1 и плоскостью (АВС); между прямой BA1 и плоскостью (AE1D1); между прямой АА1 и плоскостью (АF1D1)
Ответы
Правильная шестиугольная призма - в основании правильный шестиугольник, боковые ребра перпендикулярны основанию.
Угол между прямой и плоскостью - угол между прямой и ее проекцией.
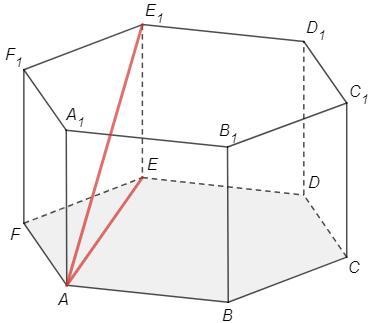
1) EE1⊥(ABC) => AE - проекция наклонной AE1 на плоскость (ABC)
∠E1AE - угол между AE1 и (ABC)
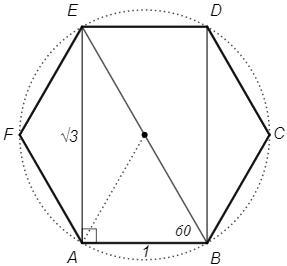
∠ABE=60 (правильный шестиугольник)
AE =AB tg(ABE) =1*tg60 =√3
tg(E1AE) =EE1/AE =1/√3 => ∠E1AE=30°
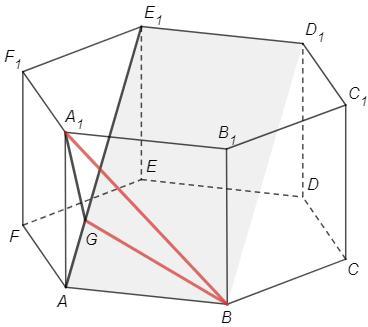
2) ABDE и ABD1E1 - прямоугольники (ABDE - проекция ABD1E1)
=> AB⊥AE1, AB⊥AE => AB⊥(AEE1)
Опустим A1G⊥AE1
AB⊥(AEE1) => AB⊥A1G
A1G⊥AB, A1G⊥AE1 => A1G⊥(AE1D1)
∠A1BG - угол между BA1 и (AE1D1)
∠E1AE=30 => ∠A1AG=60
A1G =AA1 sin(A1AG) =1*sin60 =√3/2
BA1=√2 (диагональ квадрата)
sin(A1BG) =A1G/BA1 =√3/2 :√2 =√6/4
∠A1BG =arcsin√6/4 ~37,76°
3) Аналогично пункту 2
ACDF и ACD1F1 - прямоугольники => AC⊥(FAA1)
Опустим A1H⊥AF1
AC⊥(FAA1) => AC⊥A1H
A1H⊥AF1, A1H⊥AC => A1H⊥(AF1D1)
∠A1AF1 - угол между AA1 и (AF1D1)
∠A1AF1=45° (AF1 - диагональ квадрата)