Предмет: Геометрия,
автор: kmetsanek14
Помогите пожалуйста!!
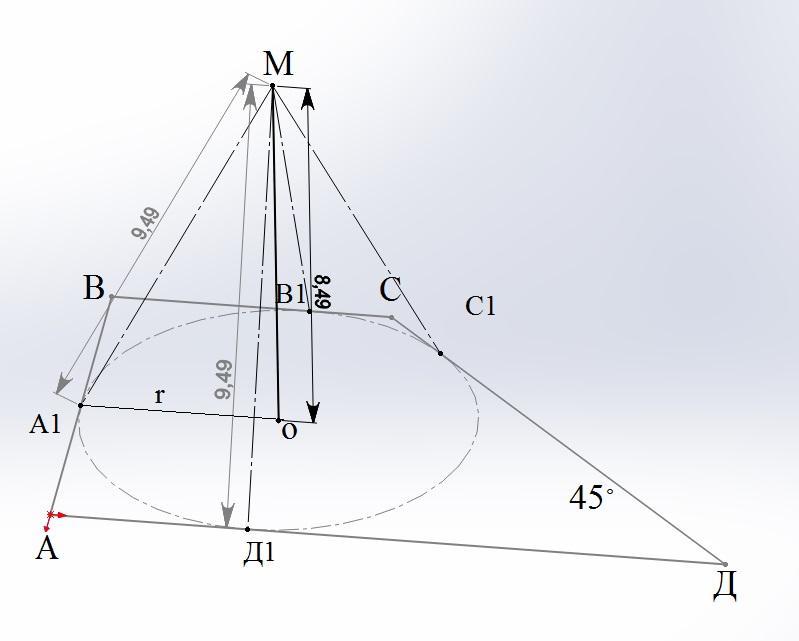
Точка О - центр кола, вписаного в трапецію ABCD, BC || AD, AB перпендикулярно до AD, CD = 12 см, кут ADC = 45°. Відрізок MO – перпендикуляр до площини трапеції. Точка M віддалена від площини трапеції на 6√2 см. Знайдіть відстань від точки M до сторін трапеції.
Ответы
Автор ответа:
2
Ответ:
А₁М=В₁М=С₁М=Д₁М=9,5 см
Объяснение:
Радиус вписанной окружности = АВ/2
АВ=СД*sin45°=12*sin45°=8,5 см
r=АВ/2=8,5/2=4,24 см
Расстояния до всех сторон одинаковые и равны гипотенузе А₁М, В₁М, С₁М, Д₁М
А₁М=√(ОМ²+r²)=√((6√2)²+4,24²)=9,5 см
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: аня1786
Предмет: Русский язык,
автор: мериет
Предмет: Окружающий мир,
автор: Аноним
Предмет: Алгебра,
автор: elenohka2003