Предмет: Алгебра,
автор: yanafoks
упростить выражения.
даю 40 баллов.
Приложения:
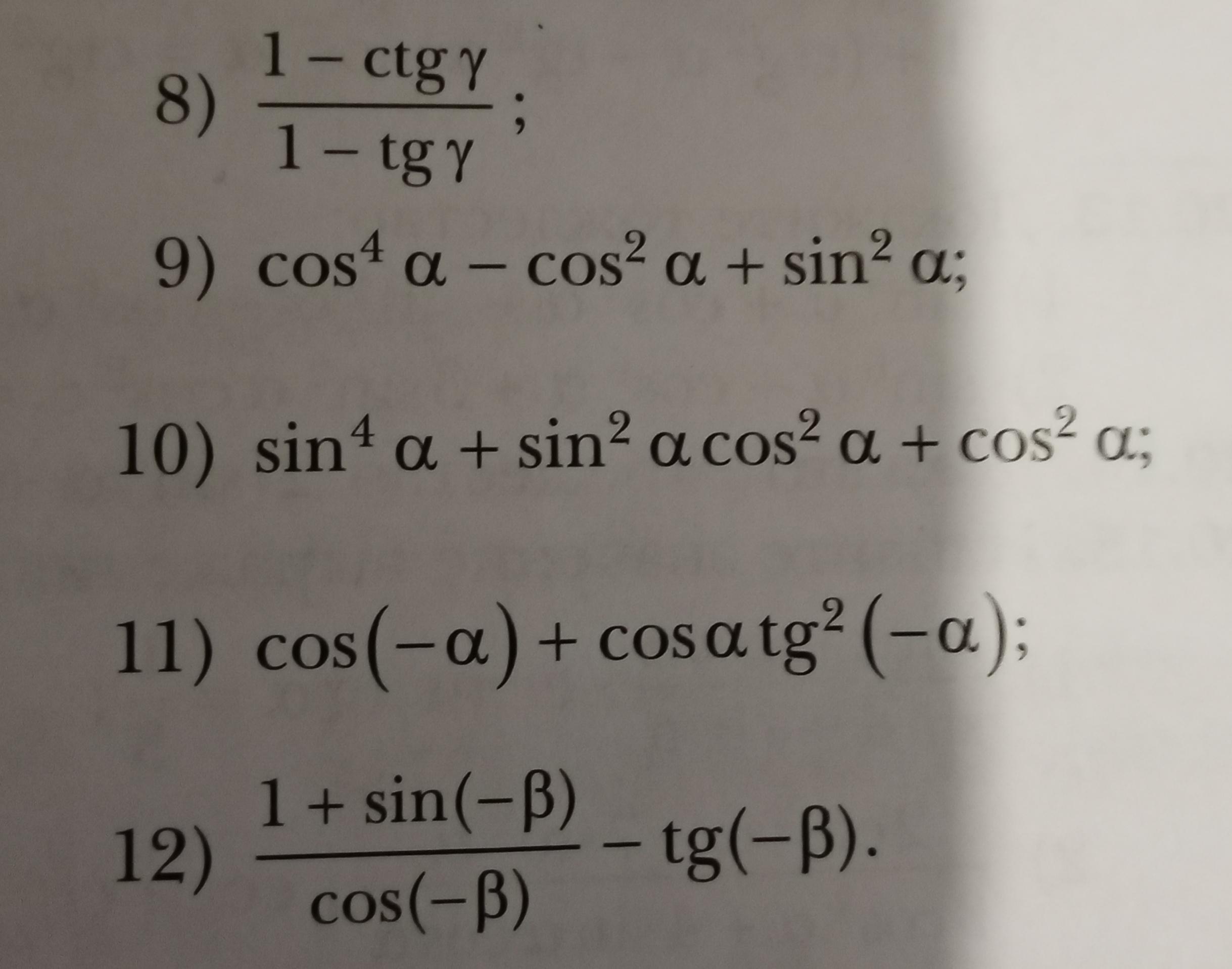
Ответы
Автор ответа:
1
Ответ:
8.
В начале вывели 1-ctga, как 1-1/tga и дали общий множитель tga
9.
(По формуле cos²a-sin²a=cos2a
10.
Если что sin²a+cos²a=1
11.
12.
Похожие вопросы
Предмет: Русский язык,
автор: ДиасБ
Предмет: Английский язык,
автор: tany19821
Предмет: Қазақ тiлi,
автор: жжжж4
Предмет: Русский язык,
автор: minakova22
Предмет: Литература,
автор: анастясия777