50 баллов
Напишите все способы, которыми можно решить уравнение ниже
21+10t-t^2=0
Ответы
Ответ:
1) Решение через дискриминант .
2) Решение с помощью выделения полного квадрата .
3) Решение с помощью теоремы Виета.
Второе уравнение фактически получили такое же, как и было задано . Подобрать корни без решения уравнения через дискриминант в этом случае сложно . Поэтому реально работают первые два способа решения .
P.S. Легко подобрать корни по теореме Виета , например, для такого уравнения .
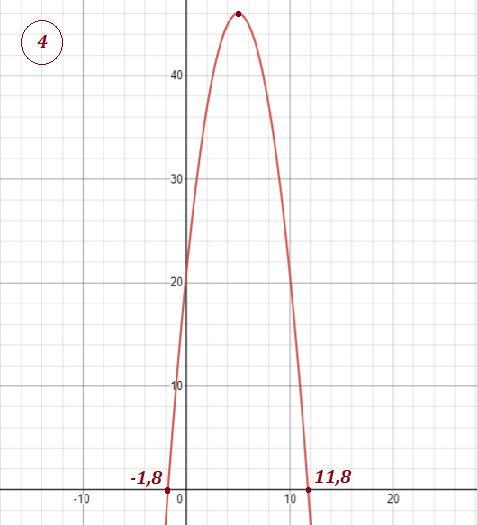
4) Графический способ решения уравнения . Построить параболу и найти точки пересечения с осью ОХ . Но в данном случае точные значения найти практически невозможно. Только приближённые значения : .
Ответ: t=5+√46; t=5-√46;
Объяснение:
1) 21+10t-t²=0
-21-10t+t²=0
по формуле для приведенного кв. уравнения
t=5±√(25+21)=5±√46; t=5+√46; t=5-√46;
2) по общей формуле корней через дискриминант. ответ тот же.
(10±√(100+84))/2=(10±2√46)/2=5±√46; t=5-√46; t=5+√46;
3) выделением полного квадрата
(t-5)²=46
It-5I=√46; t-5=±√46; t=5+√46; t=5-√46;
4) строить не буду, но приведу пример, графический метод решения. правда. в нем есть и минус. не всегда дает точное решение.