Question

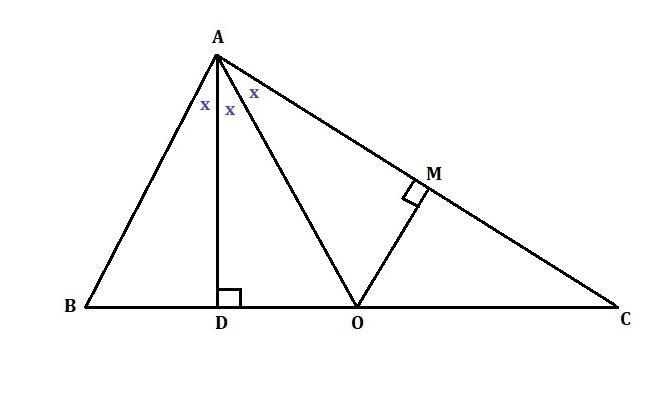
Висота і медіана, проведені з однієї вершини трикутника,розділили його кут на три рівні частини. Знайдіть кути трикутника.​

Answer 1

Ответ:

∠С=30°,∠А=90°,∠В=60°

Объяснение:

Дано: AD⊥BC, ВО=ОС. ∠ВАD=∠DАО=∠ОАС

Найти: ∠А,∠В,∠С ΔАВС

Пусть ∠ВАD=∠DАО=∠ОАС=х

1) Рассмотрим ΔВАО. АD - высота. ∠ВАD=∠DАО ⇒ АD - биссектриса.

Если в треугольнике медиана совпадает с биссектрисой, то треугольник равнобедренный. ⇒ΔВАО - равнобедренный. В равнобедренном треугольнике высота является также медианой. ⇒

ВD=DО= $\frac{1}{2}$ ВО= $\frac{1}{2}$ОС.

2) Дополнительное построение: Проведём ОМ⊥АС.

Рассмотрим прямоугольные треугольники АDО и АМО.

∠DАО=∠ОАС - по условию, АО - общая.

• Если гипотенуза и острый угол одного треугольника соответственно равны гипотенузе и острому углу другого треугольника, то такие прямоугольные треугольники равны.

⇒ΔАDО = ΔАМО

Из равенства треугольников следует равенство катетов:

DО = МО =$\frac{1}{2}$ ВО= $\frac{1}{2}$ОС.

3) Рассмотрим прямоугольный треугольник ОМС (∠М=90°).

Из доказанного выше МО=$\frac{1}{2}$ОС. Т.е. катет МО равен половине гипотенузы ОС.

• Если в прямоугольном треугольнике один из катетов равен половине гипотенузы, то этот катет лежит против угла в 30°.

Следовательно ∠С=30°

4) Рассмотрим прямоугольный треугольник АDC(∠D=90°).

По свойству острых углов прямоугольного треугольника

∠DАС=90°-∠С=90°-30°=60°.

По условию ∠DАС=2х ⇒ 2х=60°, х=30°

5) ∠ВАС=3х=3*30°=90°

∠А треугольника АВС = 90°

Так как сумма углов треугольника равна 180°, то ∠В треугольника АВС будет равен: ∠В=180°-∠А-∠С=180°-90°-30°=60°