Question

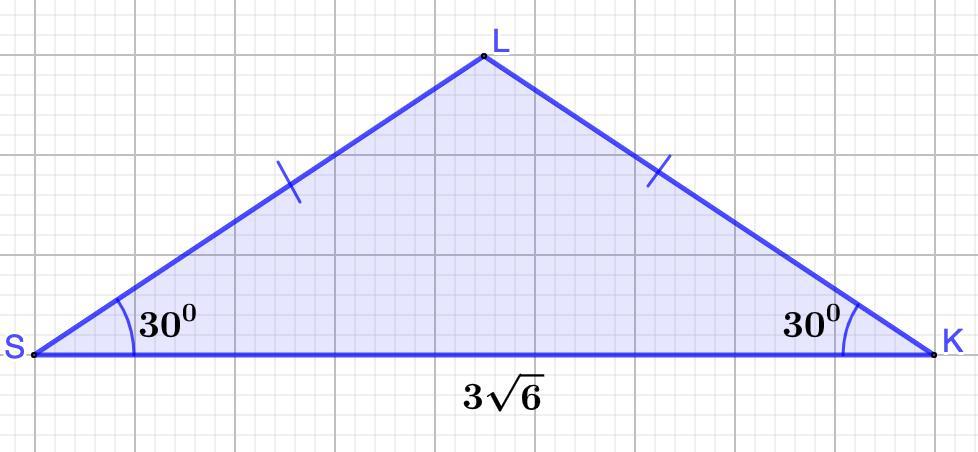
Реши равнобедренный треугольник LKS LKS, если углы при основании равны 30°, а длина основания KS = 3корня из 6

Answer 1

Ответ:

Решение равнобедренного треугольника:

∠L = 120°; SL = LK = 3√2 (ед)

Пошаговое объяснение:

Надо решить равнобедренный треугольник.

• Решить треугольник - это значит найти неизвестные стороны и углы.

Дано: ΔLKS - равнобедренный;

KS = 3√6   - основание;

∠К = ∠S = 30°;

Найти: ∠L; KL; KS.

Решение:

1. Найдем ∠L.

• Сумма углов треугольника равна 180°.

Два угла нам известны : ∠К = ∠S = 30°.

Найдем третий:

∠L = 180° - (∠K + ∠S) = 180° - (30° + 30°) = 120°

2. Найдем боковую сторону SL.

Воспользуемся теоремой синусов:

• Стороны треугольника пропорциональны синусам противолежащих углов.

⇒

$\displaystyle \frac{SL}{sin\angle{K}} =\frac{KS}{sin\angle{L}}$

Подставим значения и найдем SL.

Используем основное свойство пропорции:

• Произведение крайних равно произведению средних.

$\displaystyle \frac{SL}{sin\;30^0} =\frac{3\sqrt{6} }{sin\;120^0} \\\\SL*sin120^0=3\sqrt{6}*sin\;30^0$

Значение синусов:

$\displaystyle sin\;30^0 = \frac{1}{2}$

По формуле приведения:

$\displaystyle sin\;120^0=sin(180^0-60^0)=sin\;60^0=\frac{\sqrt{3} }{2}$

Получим уравнение:

$\displaystyle SL*\frac{\sqrt{3} }{2}=3\sqrt{6}*\frac{1}{2}\;\;\;|*2\\\\SL*\sqrt{3}=3\sqrt{6}\;\;\;|:\sqrt{3}\\\\SL=3\sqrt{2}$

Таким образом, мы решили треугольник:

SL = LK = 3√2 (ед);  ∠L = 120°.