Question

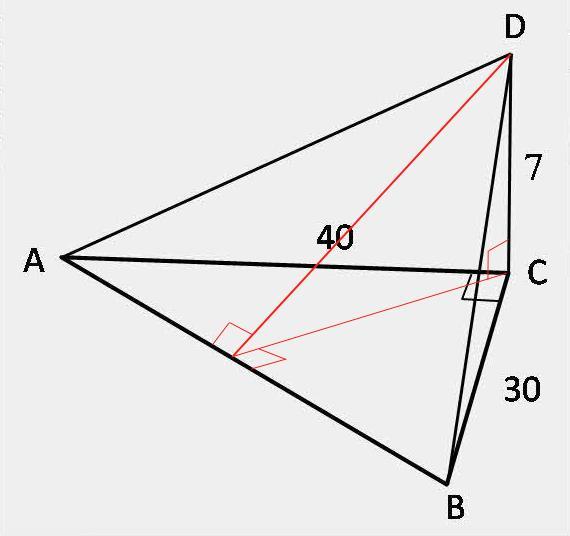
Прямая DC перпендикулярна плоскости, в которой лежит треугольник АВС. Причем, DC = 7, AC = 40, BC = 30. Найдите расстояние от точки D до прямой АВ.

Срочно!! Даю максимум баллов

Answer 1

Ответ: 25 (ед. длины).

Объяснение:

   Если прямая перпендикулярна плоскости, то она перпендикулярна к любой прямой, лежащей в этой плоскости. => DC перпендикулярна  высоте СН прямоугольного ∆ АВС.

    Расстояние от точки до прямой измеряется длиной отрезка, проведенного перпендикулярно от точки к данной прямой.

  Высота СН - проекция наклонной DH.

По т. о 3-х пп СН⊥АВ => DH⊥АВ, DH - искомое расстояние.

Решение.

DH найдем через площадь ∆ АВС и его высоту СН.

Ѕ(АВС)=АС•ВС/2

Ѕ(АВС)=СН•АВ/2 ⇒ АС•ВС=СН•АВ

АВ=√(АС²+ВС²)=√(40²+30²)=50

АС•ВС=40•30=1200

СН=АС•ВС:АВ=1200:50=24

DH=√(DC^2+CH^2)=√(49+576)=25

DH=25.