Предмет: Алгебра,
автор: anna210105
Обчисліть визначений інтеграл:
Приложения:
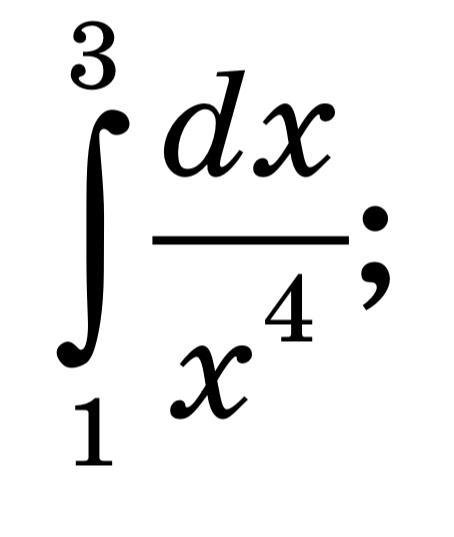
Ответы
Автор ответа:
0
Ответ:
Объяснение:
/
____
Похожие вопросы
Предмет: Русский язык,
автор: FrogHour
Предмет: Немецкий язык,
автор: Pakomov
Предмет: Русский язык,
автор: Mikalaaa
Предмет: Қазақ тiлi,
автор: siamedenov
Предмет: Английский язык,
автор: TeroVaderTV