Question

Высота опущенная из тупого угла равнобедренной трапеции делит основание на 7 см и 2см. Найдите длину средней линии трапеции.

Пожалуйста помогите!!!

Answer 1

Ответ:

7см

Объяснение:

Дано:

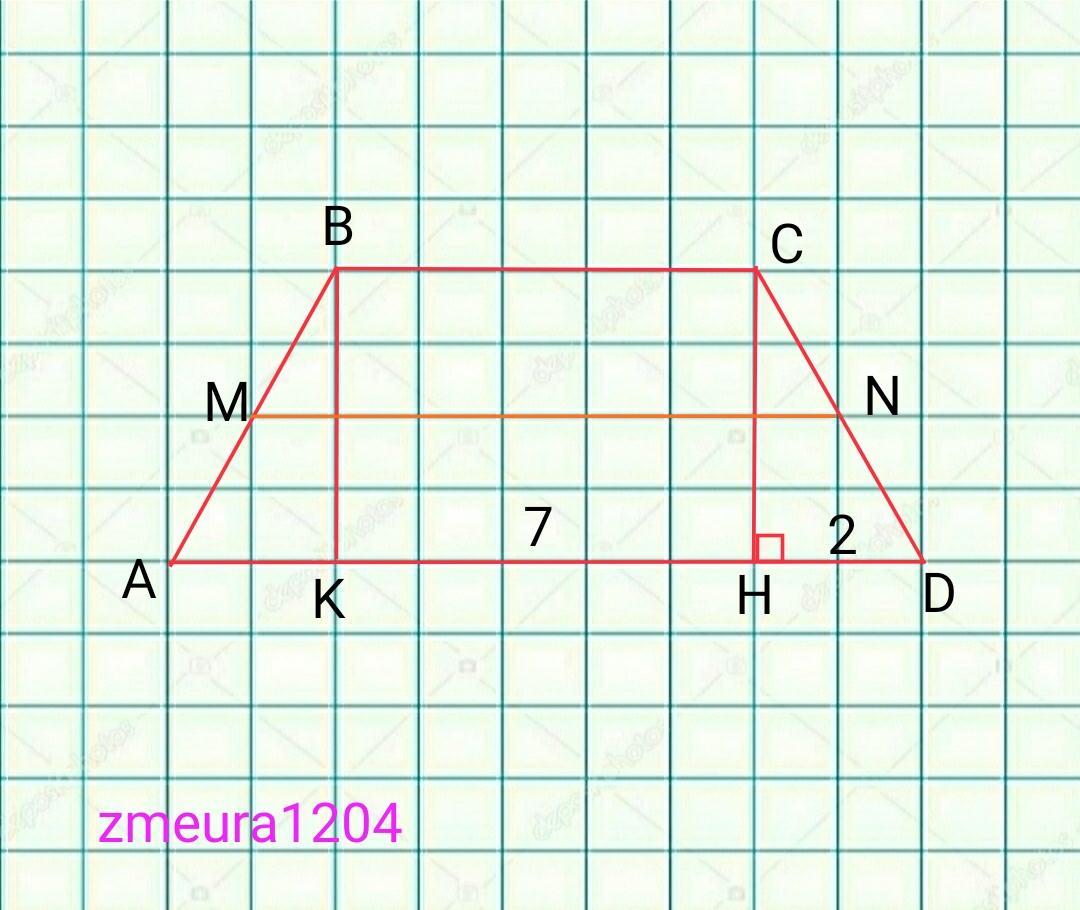
ABCD- трапеция

АВ=CD

HD=2см

АН=7см

МN=?

Решение.

Проведем высоту ВК.

АК=НD=2см

КН=AH-AK=7-2=5см

ВС=КН=5см.

AD=AH+HD=7+2=9см

MN=(BC+AD)/2=(9+5)/2=14/2=7см

Answer 2

Ответ:

14 см

Объяснение:

Для решения задачи опустим по высоте из каждого тупого угла. Трапеция разделится на два равных прямоугольных треугольника (по гипотенузе, т.к. трапеция равнобедренная, и катету-высоте) и прямоугольник. По условию получаем, что второй катет каждого треугольника 2, а его сумма со стороной прямоугольника - 7, значит сторона прямоугольника 7 - 2 = 5. Противоположные стороны прямоугольника равны ⇒ верхнее основание трапеции равно 5. Нижнее - 2 + 2 + 5 = 9 (т.к. оно состоит из стороны прямоугольника, равной 5, и двух катетов по 2). Средняя линия трапеции равна полусумме оснований, т.е. 5 + 9 = 14 см.