Задача 4. Дано общее уравнение кривой второго порядка. Требуется
а) преобразовать уравнение к каноническому виду;
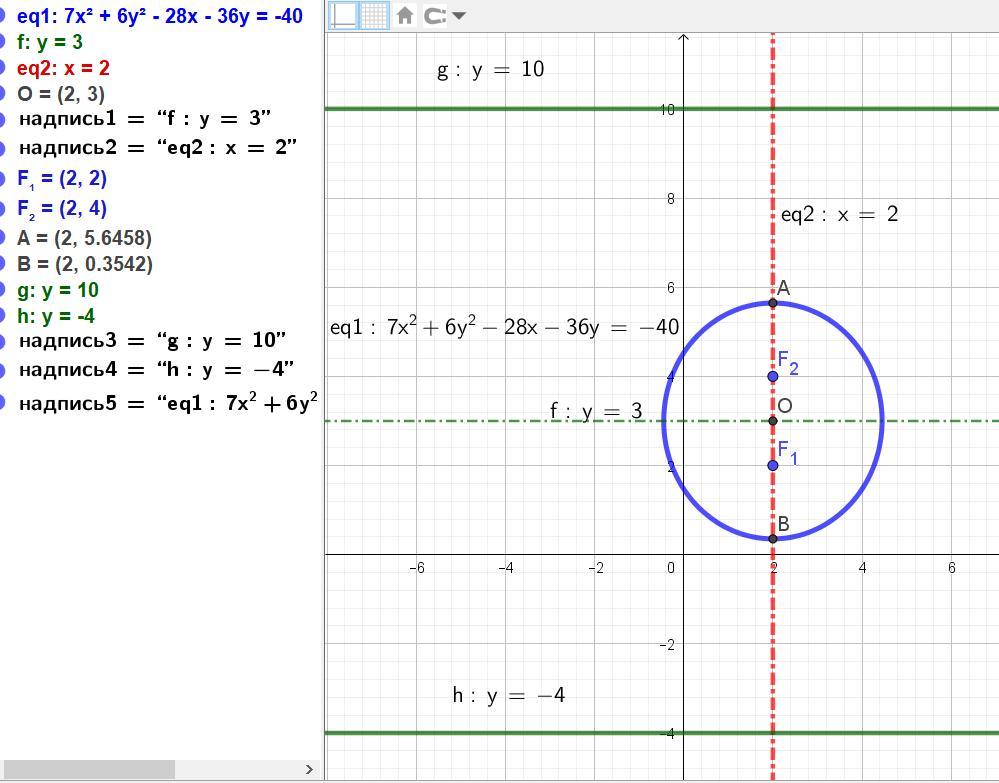
б) схематически построить кривую.
7x^2 + 6y^2 - 28x - 36y + 40=0
Ответы
Выделяем полные квадраты:
для x:
7(x²-2·2x + 2²) -7·2² = 7(x-2)²-28
для y:
6(y²-2·3y + 3²) -6·3² = 6(y-3)²-54
В итоге получаем:
7(x-2)²+6(y-3)² = 42
Разделим все выражение на 42.
(x – 2)²/6 + (y – 3)²/7 = 1 или
(x – 2)²/(√6)² + (y – 3)²/(√7)² = 1.
Данное уравнение определяет эллипс с центром в точке:
C(2; 3)
4. Параметры кривой.
Полуоси эллипса: a = √6, b = √7.
Так как значение b больше a, то фокусы эллипса располагаются на оси, параллельной координатной оси Оу:
Найдем координаты фокусов F1(-c;0) и F2(c;0), где c - половина расстояния между фокусами
c = √(b² - a²) = √(7 – 6) = √1 = 1.
F1(0;-1), F2(0;1).
С учетом центра, координаты фокусов равны:
F1(2;-1+3), F2(2;1+3) = F1(2; 2), F2(2; 4).
Тогда эксцентриситет будет равен:
e = c/b = 1/√7.
Вследствие неравенства c < a эксцентриситет эллипса меньше 1.
Уравнения директрис для данного эллипса:
y = yo +-(b/e).
Подставив данные, получаем:
у1 = 3 - (√7/(1/√7) = 3 - 7 = -4,
у2 = 3 + (√7/(1/√7) = 3 + 7 = 10.
Более подробное решение с применением инвариантов дано во вложении.