Помогите пожалуйста, уж в геометрии не разбираюсь от слова совсем))
Задание 1.
Определите, существует ли правильный многоугольник, угол которого равен 135°.
Задание 2.
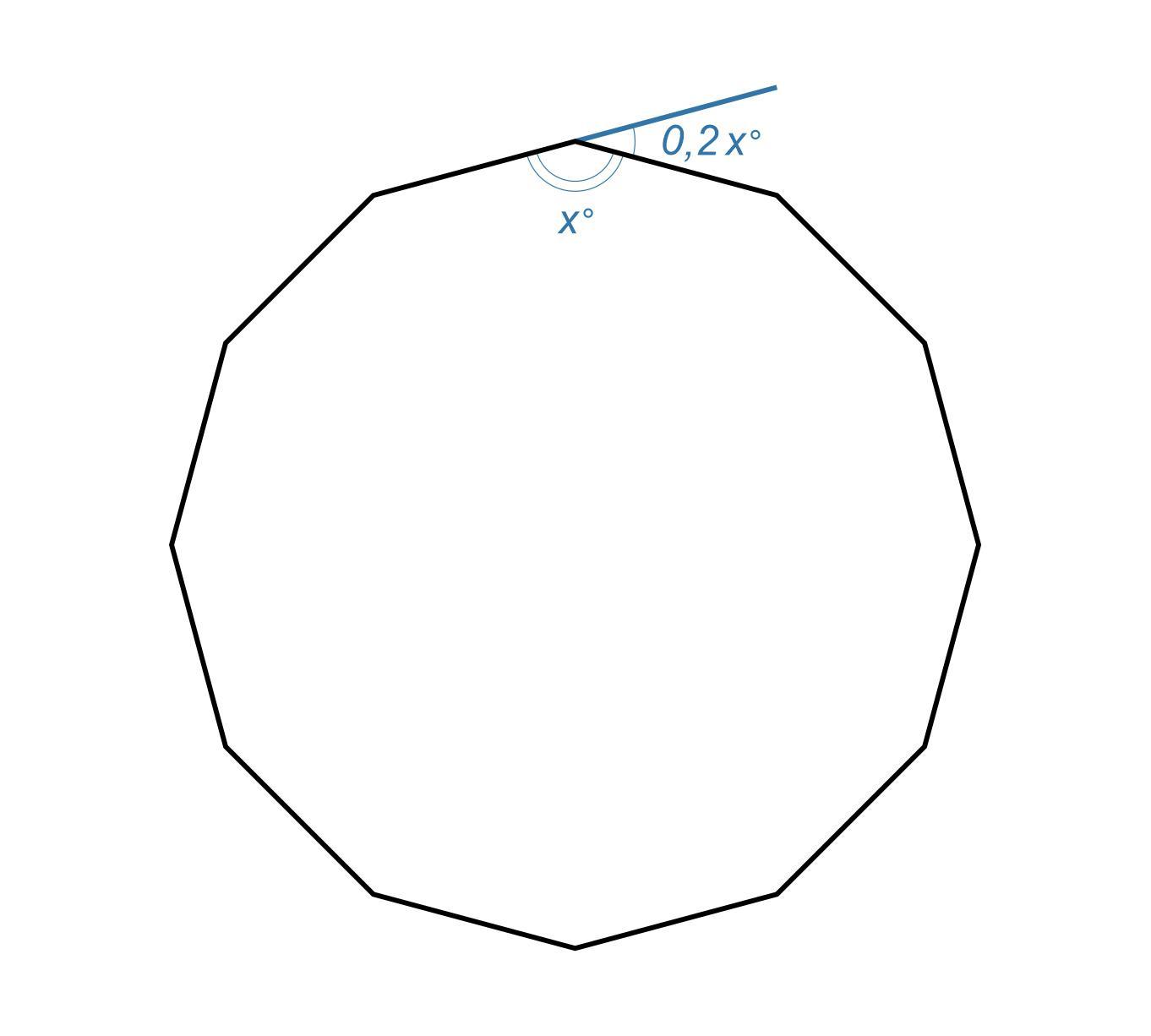
Определите количество сторон правильного многоугольника, если угол, смежный с внутренним углом многоугольника, составляет 0,2 угла многоугольника.
Задание 3.
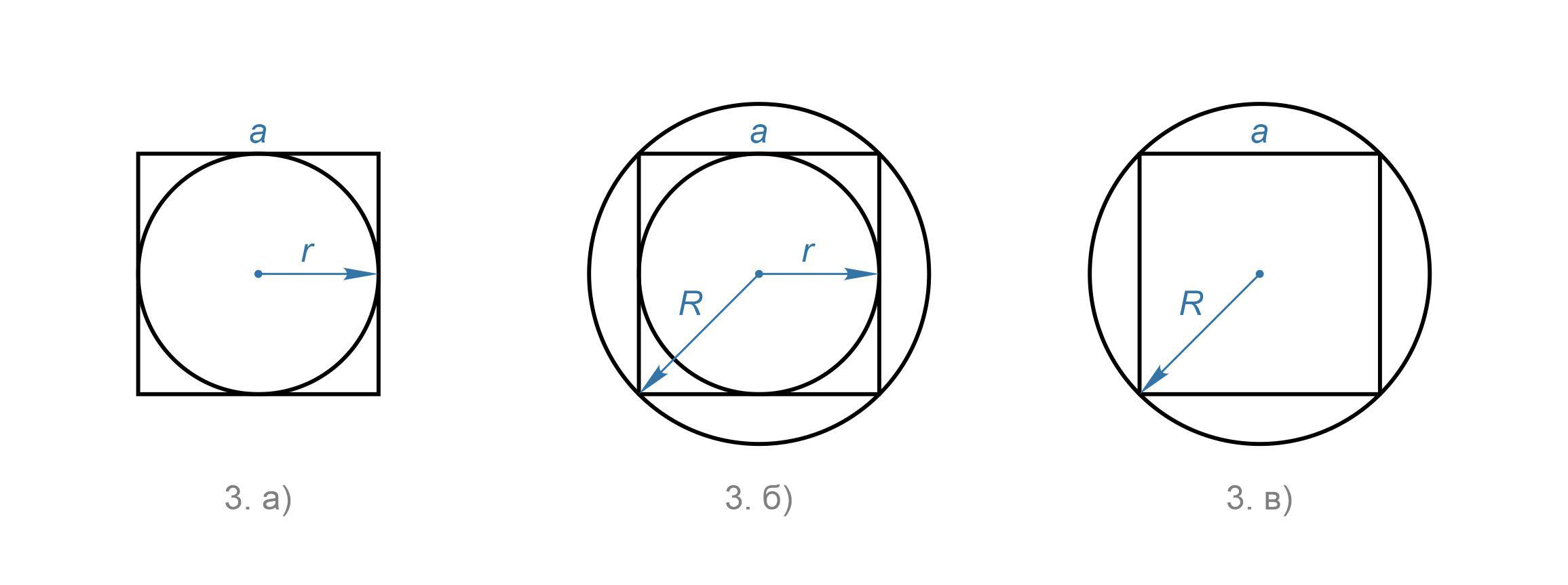
Задан правильный многоугольник, в котором n = 4. Найдите:
а) площадь многоугольника, если радиус вписанной окружности равен 4 см;
б) радиус вписанной окружности, если радиус описанной окружности равен 8 см;
в) периметр многоугольника, если радиус описанной окружности равен 1,1.jpg.png см.

Ответы
Задание 1
Ответ: Да, существует. Это правильный 8-ми угольник (см. картинку №1).
Объяснение:
Известно что сумма внутренних углов выпуклого многоугольника S равна произведению 180° на количество сторон n без двух:
S = 180°(n-2)
Т.к. сумма внутренних углов выпуклого многоугольника = внутреннему углу, помноженному на количество сторон ⇒
S = 135° × n
Отсюда выходит что:
135n = 180(n-2)
Находим n:
135n = 180n - 360
180n - 135n = 360
45n = 360
n = 360 ÷ 45
n = 8 (количество сторон правильного многоугольника)
Задание 2
Ответ: Количество сторон правильного многоугольника = 12 (см. картинку №2).
Объяснение:
Пускай внутренний угол правильного многоугольника = x°
⇒ смежный с ним угол = 0,2x°
Смежные углы — это пара углов, у которых одна сторона общая, а две другие стороны лежат на одной прямой. Следовательно, два смежных угла составляют развёрнутый угол = 180°.
⇒ x + 0,2x = 180
1,2x = 180
x = 180 ÷ 1,2
x = 150° (внутренний угол выпуклого многоугольника)
Известно что сумма внутренних углов выпуклого многоугольника S равна произведению 180° на количество сторон n без двух:
S = 180°(n-2)
Т.к. сумма внутренних углов выпуклого многоугольника = внутреннему углу, помноженному на количество сторон ⇒
S = 150° × n
Отсюда выходит что:
150n = 180(n-2)
Находим n:
150n = 180n - 360
180n - 150n = 360
30n = 360
n = 360 ÷ 30
n = 12 (количество сторон правильного многоугольника)
Задание 3
а) Ответ: Площадь многоугольника = 64 см².
Объяснение:
Правильный многоугольник, в котором n = 4 это КВАДРАТ.
Диаметр окружности d = 2r, где r - радиус
Известно что сторона квадрата a равна диаметру d вписанной в него окружности
⇒ d = a = 2r = 2×4 = 8 cm.
Площадь квадрата = a² = 8² = 64 cm²
б) Ответ: Радиус вписанной окружности см.
Объяснение:
Известно что сторона квадрата , где r - радиус вписанной окружности.
Так же известно что сторона квадрата , где R - радиус описанной окружности ⇒
(радиус вписанной окружности)
в) Ответ: Периметр многоугольника = 16 см.
Объяснение:
Известно что сторона квадрата , где R - радиус описанной окружности
⇒
Периметр любого многоугольника P = n·a, где a - сторона многоугольника, n - количество его сторон.
⇒ P = 4 × 4 = 16 cm