Question

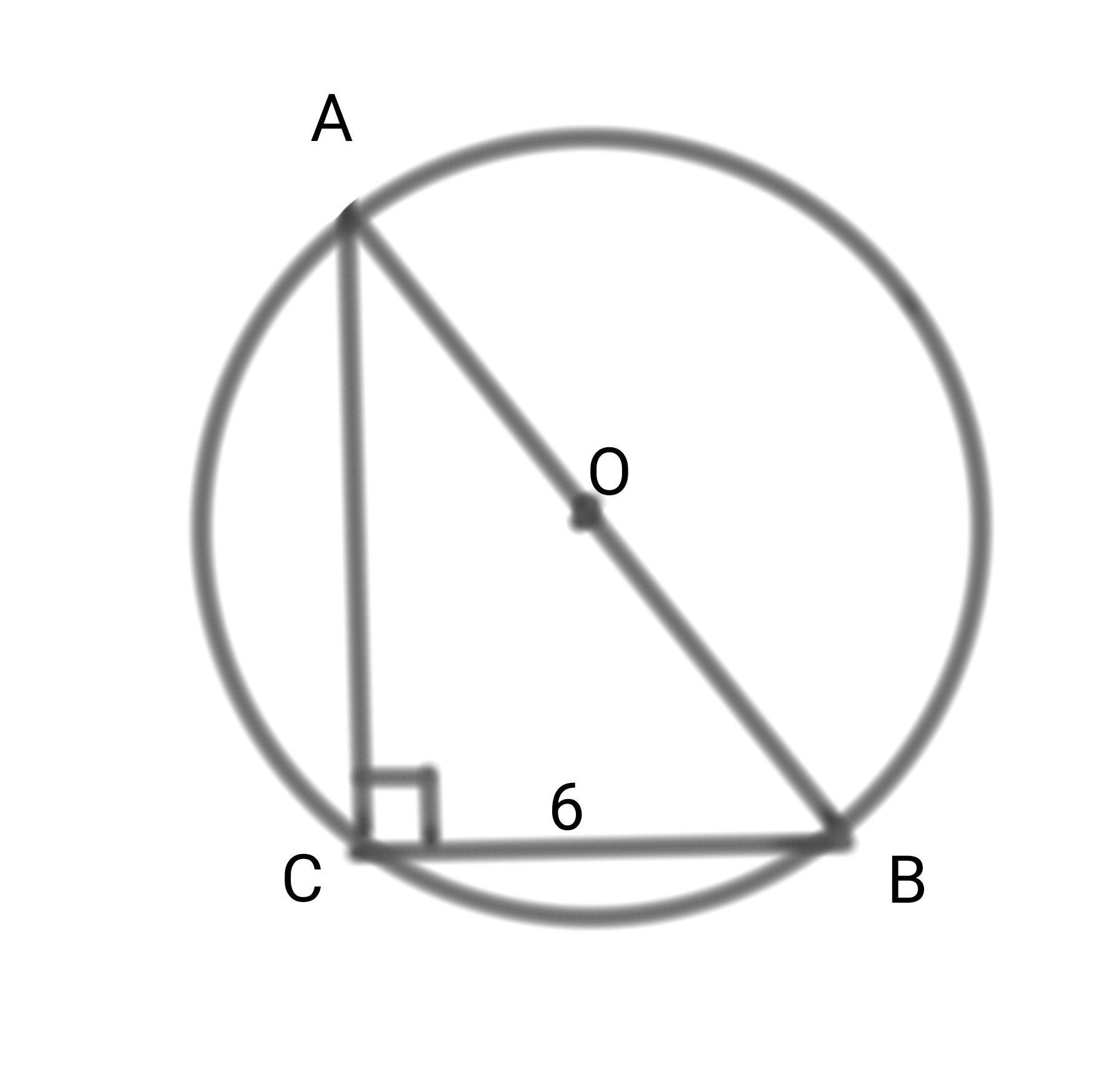
в прямоугольном треугольнике ABC угол C равен 90° BC равен 6 косинус A 3/5. найти радиус окружности описанной около треугольника .
ПОМОГИТЕ ПРОШУ .заранее спасибо ;)))​

Answer 1

Ответ:

Точка O — центр описанной окружности, находится в центре гипотенузы AB.

Найдем синус угла A по формуле

$\sin( \alpha ) = \sqrt{1 - \cos^{2} ( \alpha ) }$

$\sin(A) = \sqrt{1 - {( \frac{3}{5} )}^{2} } = \sqrt{1 - \frac{9}{25} } = \sqrt{ \frac{16}{25} } = \frac{4}{5}$

Синус это отношение противолежащего катета на гипотенузу

$\sin(A) = \frac{BC}{AB}$

$\frac{4}{5} = \frac{6}{AB} \\ AB = \frac{6 \times 5}{4} = \frac{30}{4} = 7 \frac{2}{4} = 7.5$

Радиус равен половине гипотенузы.

$R = \frac{7.5}{2} = 3.75$

Answer 2

Ответ:

Объяснение:

SinA=√(1-cos²A)=4/5;

2R=BC/sinA - теорема синусов;

2R= 7,5;

R=7,5/2=3,75 ед.