Предмет: Математика,
автор: BloodRainbow
Помогите решить, найти y' и y''.
Приложения:
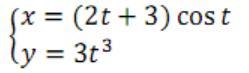
Ответы
Автор ответа:
3
Ответ:
Производная первого порядка :
Производная второго порядка :
Пошаговое объяснение:
Надо найти производные первого и второго порядка от функции, заданной параметрически.
Найдем производную первого порядка по формуле:
1. Найдем производную первого порядка .
Производную произведения найдем по формуле:
Также воспользуемся формулами:
⇒
2. Найдем производную второго порядка по формуле:
Нам понадобится формула производной частного:
Также
Найдем производную :
3. Найдем производную второго порядка :
versachexdior:
можете помочь мне
Похожие вопросы
Предмет: Русский язык,
автор: татьянаилья
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: 62rabiga
Предмет: Русский язык,
автор: arsenkrol
Предмет: Биология,
автор: mikku16