Предмет: Геометрия,
автор: starik97
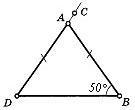
Найдите величину угла САВ, если сумма всех углов треугольника равна 180°.
Приложения:
marshal500:
САВ внешний, величина внешнего угла равны сумме углов не смежных с ним, треугольник равнобедренный, значит САВ=50+50=100...
Ответы
Автор ответа:
1
Ответ:
Треугольник равнобедренный, поэтому угол D равен углу B.
Угол DAB=80°.
Автор ответа:
2
Ответ:
100°
Объяснение:
Внешний угол треугольника равен сумме внутренних углов, не смежных с ним.
∠САВ=∠В+∠D
∠D=∠B=50° по условию, т.к. АВD - равнобедренный.
∠САВ=∠В+∠D=50+50=100°
Похожие вопросы
Предмет: Қазақ тiлi,
автор: камилла180
Предмет: Русский язык,
автор: СмертьТапочка
Предмет: Русский язык,
автор: Аноним
Предмет: Информатика,
автор: kateblinuuu
Предмет: Физика,
автор: LapikaDorra2005