Предмет: Алгебра,
автор: ivankovryazhneckav
Помогите плз! Дам 30 баллов
Приложения:
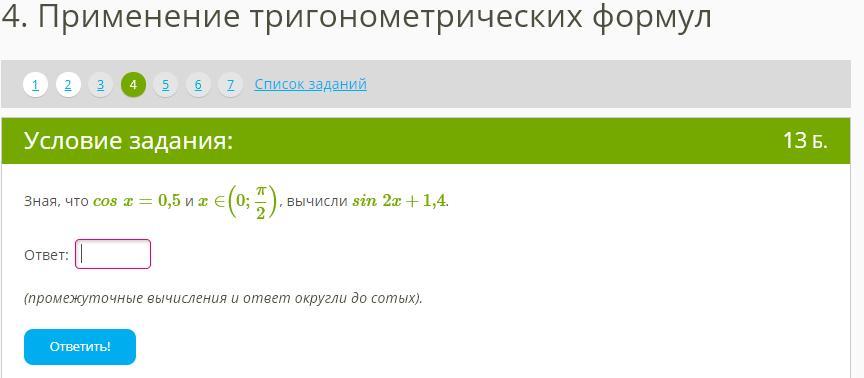
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Дано:
Найти:
Решение:
ivankovryazhneckav:
Спасибо большое! Не мог бы ты помочь еще с похожим заданием у меня в профиле?
Похожие вопросы
Предмет: Английский язык,
автор: 26Уля
Предмет: Русский язык,
автор: викукуська
Предмет: Окружающий мир,
автор: bmxmaster0604
Предмет: Русский язык,
автор: ilovemera
Предмет: Окружающий мир,
автор: magics51