Question

Помогите пожалуйста срочно ​

Answer 1

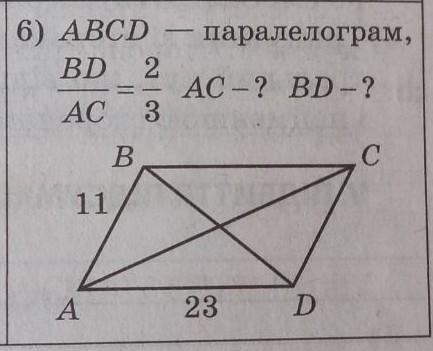
Решение основано на теореме косинусов.

Пусть BD = x, AC = y. По условию у = 3х/2.

Из треугольника ABD находим:

cos A = (11² + 23² - x²)/(2*11*23).

Из треугольника ACD находим:

cos D = (11² + 23² - y²)/(2*11*23).

Приравняем эти значения с учётом, что косинус угла D = -cos A и у = 3х/2.

(11² + 23² - x²)/(2*11*23) = -((11² + 23² - (9x²/4)/(2*11*23)),

11² + 23² - x² = -11² - 23² + (9x²/4),

(9x²/4) + x² = 2*11² + 2*23²,

13x² = 8*11² + 8*23² = 968 + 4232 = 5200,

x² = 5200/13 = 400,

х = √400 = 20.

То есть BD = 20, AC = (3/2)*20 = 30.

Ответ: BD = 20, AC = 30.