Предмет: Алгебра,
автор: Clipipaster
Помогите с геометрией! Даю 40 баллов!
Приложения:
Ответы
Автор ответа:
2
Ответ:
Теорема синусов: .
dDeVoChKa:
Добрый вечер! Спасибо за решение! Не могли бы Вы, пожалуйста, помочь мне так же с решением? У меня в последнем "Добавленном" есть пример. Заранее спасибо!
Автор ответа:
0
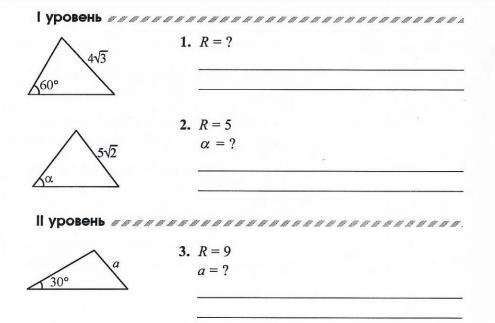
1. по следствию из теоремы синусов отношение стороны к синусу противолежащего угла равно двум радиусам, т.е. диаметру описанной окружности, поэтому, чтобы найти радиус, надо сторону разделить на удвоенный синус противолежащего угла. т.е. R=4√3/(2sin60°)=4√3/(2*√3/2)=4
2. по тому же следствию найдем sinα=а/2R=5√2/(2*5)=√2/2⇒α=45°
3. по тому же следствию найдем а=2Rsinα=2*9*2sin30°=2*9*0.5=9
Похожие вопросы
Предмет: Русский язык,
автор: lesya114
Предмет: Українська література,
автор: sveta1246
Предмет: Русский язык,
автор: Jana2008
Предмет: Литература,
автор: ameliypetrova
Предмет: Информатика,
автор: yulyakonkova7