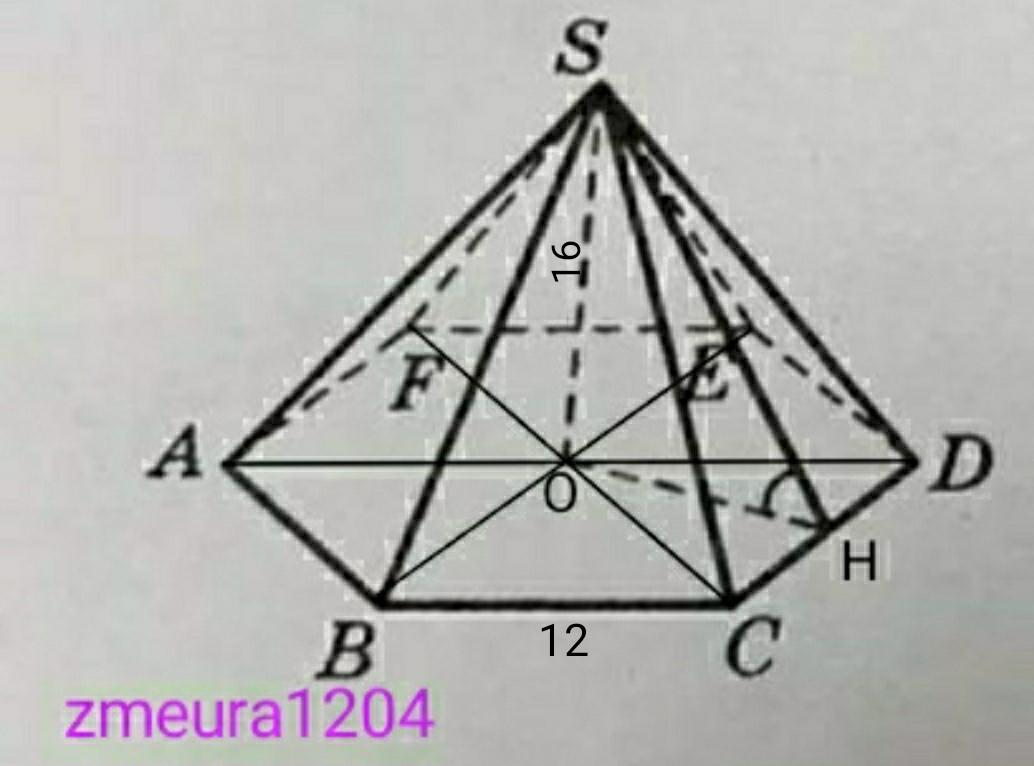
Задана правильная шестиугольная пирамида, высота которой равна 16 см, а сторона основания – 12 см.
а) Определите длину бокового ребра пирамиды
б) Определите длину апофемы
в) Вычислите объём пирамиды
И напишите формулы по которым вычисляли
Ответы
Ответ:
20см длина бокового ребра;
2√91см длина апофемы пирамиды;
1152√3 см³ объем пирамиды.
Объяснение:
1)
В основании правильный шестиугольник, шестиугольник делиться на 6 равных треугольников.
∆SOА- прямоугольный треугольник
АО=12см катет
SO=16см катет
По теореме Пифагора
SA=√(AO²+SO²)=√(12²+16²)=√(144+256)=
=√400=20см. длина бокового ребра
2)
∆СОD- равносторонний треугольник
Формула нахождения высоты равностороннего треугольника
h=a√3/2, где а-сторона треугольника; h-высота (h=OH; a=CD)
OH=CD√3/2=12√3/2=6√3 см.
∆SOH- прямоугольный треугольник
SO;OH- катеты;
SH- гипотенуза (апофема пирамиды)
По теореме Пифагора
SH=√(SO²+OH²)=√(16²+(6√3)²)=
=√(256+108)=√364=2√91см. апофема пирамиды
3)
Sосн=6*АВ²√3/4=1,5*12²√3=216√3 см² площадь шестиугольника.
V=Sосн*SO/3=216√3*16/3=1152√3 см³
обьем пирамиды.