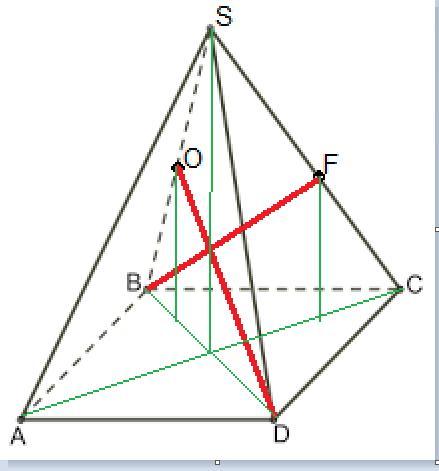
SABCD - правильная четырёхугольная пирамида, боковые ребра в 2 раза больше стороны основания, точки O и F - середины рёбер SB и SC соответственно. Вычислить косинус угла между BF и DO.
Ответы
SABCD - правильная четырёхугольная пирамида, боковые ребра в 2 раза больше стороны основания, точки O и F - середины рёбер SB и SC соответственно. Вычислить косинус угла между BF и DO.
Эту задачу можно решить двумя способами: 1) векторным и 2) геометрическим.
1) Поместим пирамиду в прямоугольную систему координат, вершиной В в начало, ребром ВА по оси Ох, ребром ВС по оси Оу.
Примем длину ребра основания, равную а = 4 (для кратности между точками).
Длина бокового ребра L = 2*4 = 8.
Высоту Н пирамиды определим как высоту равнобедренного треугольника, составленного боковыми рёбрами L и диагональю d основания. равной а√2 = 4√2.
H = √(L² - (d/2)²) = √(8² - (4√2/2)²) = √(64 – 8) = √56 = 2√14.
Определяем координаты точек.
B(0; 0; 0), F(1; 3; √14), вектор BF = (1; 3; √14),
модуль равен √(1+9+14) = √24.
D(4; 4; 0), O(1; 1; √14), вектор DO = (-3; -3; √14),
модуль равен √(9+9+14) = √32.
Находим косинус угла между этими векторами.
cos (BF_DO) = (1*(-3)+(3*(-3)+√14*√14)/(√24*√32) = 2/√(4*2*3*16*2) = 2/16√3 = 1/8√3 = √3/24.
Угол (BF_DO) = arccos(1/8√3) = 1,49856 радиан или 85,8614 градуса.