Question

ПОМОГИТЕ ПОЖАЛУЙСТА РЕШИТЬ ​

Answer 1

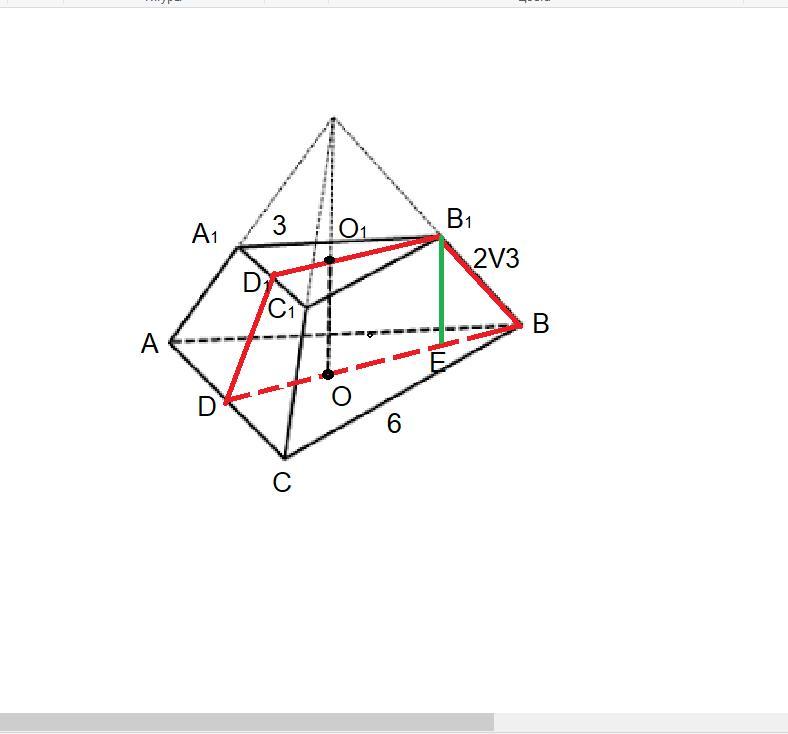
В сечении – трапеция, основания которой равны высотам оснований пирамиды.

Основания пирамиды – равносторонние треугольники, высота h которых определяется по формуле:

h = a√3/2. Подставим значения длин сторон оснований:

нижнего а = 6, верхнего а1 = 3.

BD = h = 6√3/2 = 3√3.

B1D1 = h1 = 3√3/2.

Высоту пирамиды Н = В1Е найдём по теореме Пифагора, определив сначала разность отрезков высот от центра до вершины.

О1В1 = (2/3)h1 = (2/3)*(3√3/2) = √3.

ОВ = (2/3)h = (2/3)*(3√3) = 2√3.

Отрезок ВЕ = 2√3 - √3 = √3.

Высота Н = √((2√3)² - (√3)²) = √(12 – 3) = √9 = 3.

Средняя линия L трапеции равна полусумме оснований.

L = ((3√3) + (3√3/2))/2 = 9√3/4.

Тогда площадь сечения как трапеции равна:

S = LH = (9√3/4)*3 = 27√3/4.

Ответ: площадь сечения равна 27√3/4 кв. ед.