Предмет: Геометрия,
автор: sipilovegor344
доказать теорему: если при двух прямых секущей соответственные углы равны то прямые паралельны.
Ответы
Автор ответа:
0
3. Теорема
Если при пересечении двух прямых секущей сумма односторонних углов равна 1800, то прямые параллельны.
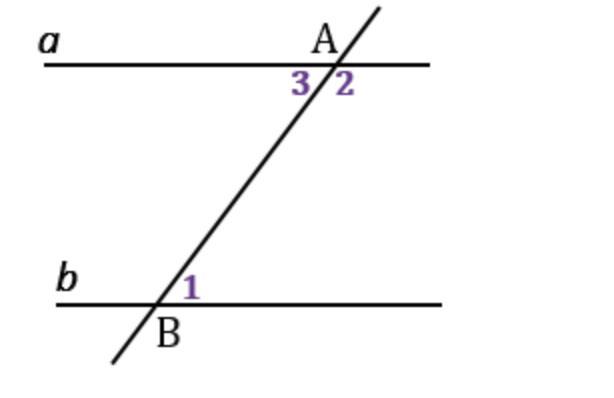
Дано: прямые и , АВ - секущая, 1 и 2 - односторонние, 1 + 2 = 1800 (Рис.7).
Доказать: .
Доказательство:
Углы 3 и 2 - смежные, значит по свойству смежных углов 3 + 2 = 1800, откуда 3 = 1800 - 2, при этом 1 + 2 = 1800, откуда 1 = 1800 - 2, тогда 1 = 3, а углы 1 и 3 накрест лежащие, следовательно, (см. теорему 1). Что и требовалось доказать.
Если при пересечении двух прямых секущей сумма односторонних углов равна 1800, то прямые параллельны.
Дано: прямые и , АВ - секущая, 1 и 2 - односторонние, 1 + 2 = 1800 (Рис.7).
Доказать: .
Доказательство:
Углы 3 и 2 - смежные, значит по свойству смежных углов 3 + 2 = 1800, откуда 3 = 1800 - 2, при этом 1 + 2 = 1800, откуда 1 = 1800 - 2, тогда 1 = 3, а углы 1 и 3 накрест лежащие, следовательно, (см. теорему 1). Что и требовалось доказать.
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: sergo2023
Предмет: Русский язык,
автор: max2344444
Предмет: Русский язык,
автор: msaturn20
Предмет: Русский язык,
автор: ViktoryaWeber
Предмет: Литература,
автор: Анастасия21032003