Предмет: Геометрия,
автор: eugenystrigulin
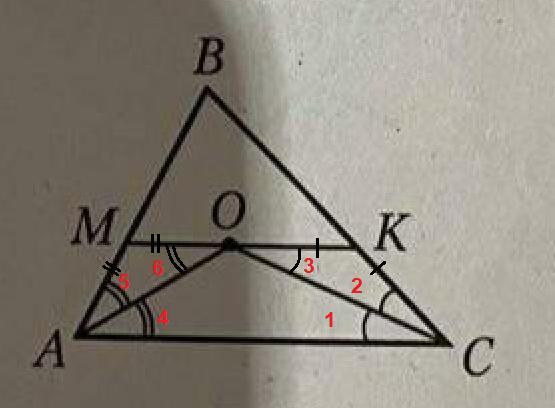
На рисунке 5 MK параллельно AC, AO и CO - биссектрисы углов BAC и BCA, AB=9см, BC = 10 см, AC=11см. Найдите периметр треугольника MBK
Приложения:

Ответы
Автор ответа:
4
Ответ:
19 см
Объяснение:
∠1 = ∠2, так как СО биссектриса угла ВСА,
∠1 = ∠3 как накрест лежащие при пересечении МК║АС секущей СО, значит ∠2 = ∠3.
В ΔКОС два равных угла, значит он равнобедренный,
ОК = КС.
∠4 = ∠5, так как АО биссектриса угла ВАС,
∠4 = ∠6 как накрест лежащие при пересечении МК║АС секущей АО, значит ∠5 = ∠6.
В ΔМОА два равных угла, значит он равнобедренный,
МО = МА.
Периметр треугольника МВК:
Р = ВМ + МК + ВК
Р = ВМ + МО + ОК + ВК
Но МО = МА и ОК = КС, значит
Р = ВМ + МА + КС + ВК = (ВМ + МА) + (КС + ВК) = АВ + ВС = 9 + 10 = 19 см
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: орзан
Предмет: Русский язык,
автор: салта22
Предмет: Другие предметы,
автор: 380680543502
Предмет: Физика,
автор: kate444ka00
Предмет: Математика,
автор: ilyacom2008