Question

здравствуйте, уважаемые эксперты! Прошу Вас ответить на следующий вопрос:
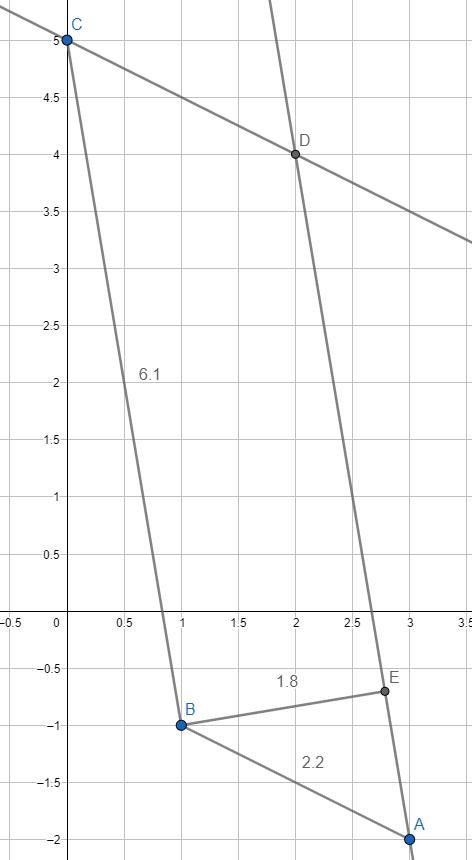
Даны три последовательные вершины параллелограмма A(3;-2), B(1;-1), C(0;5)
Не находя координаты вершины D Найти:
1) Уравнение стороны AD
2) Уравнение Высоты BK, опущенной из вершины В на сторону AD
3) длину высоты BK 4) Уравнение диагонали BD
5) тангенс угла между диагоналями параллелограмма.
Записать общее уравнения найденных прямых. Построить чертеж.

Answer 1

Ответ:

Подразумевая, что задача для 7-ого/8-ого класса попробую решить ее наиболее понятным для Вас и подробным способом:

1) По определению параллелограмма сторона AD будет параллельна стороне BC. Мы знаем, что параллельные прямые имеют одинаковый коэффициент k (то есть у них одинаковый тангенс угла наклона).

Воспользуемся этим и зададим уравнение прямой BC.

Это проще всего сделать по формуле:

$\dfrac{x-x_1}{x_2-x_1}=\dfrac{y-y_1}{y_2-y_1},\;\Rightarrow\;\dfrac{x-1}{0-1}=\dfrac{y+1}{5+1},\;\Rightarrow\;y=-6x+5,\;\Rightarrow\;k=-6$

Однако Вам может быть этот способ непривычен.

Тогда составляете систему из двух уравнений, как Вас учили и приходите к тому же самому выводу.

Обратимся теперь к уравнению $y=kx+b$. Наша прямая проходит через точку A(3; -2). Тогда $x=3,\;y=-2$. Коэффициент $k=-6$ мы нашли.

Подставим эти данные в уравнение и получим $b=y-kx=-2-(-6)\times3=16$. Тогда искомое уравнение $y=-6x+16$.

2) Прямая BK по определению высоты перпендикулярна стороне AD. Мы знаем, что в этом случае выполняется свойство $k_{AD}\times k_{BK}=-1$. Тогда $k_{BK}=\dfrac{1}{6}$. Прямая проходит через точку B(1; -1). Тогда коэффициент $b$ будет равен $-\dfrac{7}{6}$, а все уравнение имеет вид $y=\dfrac{1}{6}x-\dfrac{7}{6}$.

3) Длина высоты BK может быть получена, например путем решения системы из уравнений, записанных в пунктах 1 и 2. Но ответ будет кривой. Подобную операцию вы всегда сможете сделать сами, а я позволю себе отойти немного в сторону.

Имеем вектор $\overline{a}=\overline{(-1,\;6)},\;\overline{b}=\overline{(-2,\;1)}$. $S=|\overline{a}\times \overline{b}|=11$, $AD=|\overline{a}|=\sqrt{37}$.

Тогда $BK=\dfrac{11}{\sqrt{37}}$. Так считать намного проще.

4) Точку D здесь использовать не запрещается. D(2, 4). Откуда уравнение будет $y=5x-6$.

5) Уравнение AC: $y=-\dfrac{7}{3}x+5$. Тангенс угла будет $\dfrac{k_1-k_2}{1+k_1k_2}=-\dfrac{11}{16}$.