Question

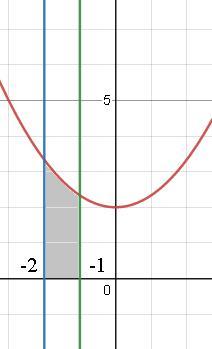
Найдите значение параметра а(а>0), при котором площадь фигуры ограниченной графиком функции у=а$x^{2}$+2 и прямыми х=-2; х=-1; у=0, равно 31/12

Answer 1

$S=\int\limits^{-1}_{-2} {(ax^2+2)} \, dx =(a\frac{x^3}{3}+2x)| ^{-1}_{-2}=a(\frac{(-1)^3}{3}-\frac{(-2)^2}{3})+2(-1-(-2))=\frac{7}{3}a+2$

По условию

$S=\frac{31}{12}$

$\frac{7}{3}a+2=\frac{31}{12}$

$\frac{7}{3}a=\frac{31}{12}-2\\\\\frac{7}{3}a=\frac{31-24}{12}\\\\\frac{7}{3}a=\frac{7}{12}\\\\a=\frac{1}{4}$

Answer 2

вам задана криволинейная трапеция. найдя ее площадь и приравняв  к 31/12 , можно ответить на ваш вопрос. итак, площадь считаем через определенный интеграл от -2 до -1 от функции (ах²+2-0) , он равен ах³/3+2х, по формуле Ньютона - Лейбница находим определенный интеграл.

S=((-1)³*а/3+2*(-1))-((-2)³*а/3+2*(-2))=-а/3-2+8а/3+4=2 +7а/3

2 +7а/3=31/12

24+28а=31

28а=7, значит. а =0.25

Ответ при а=0.25