Question

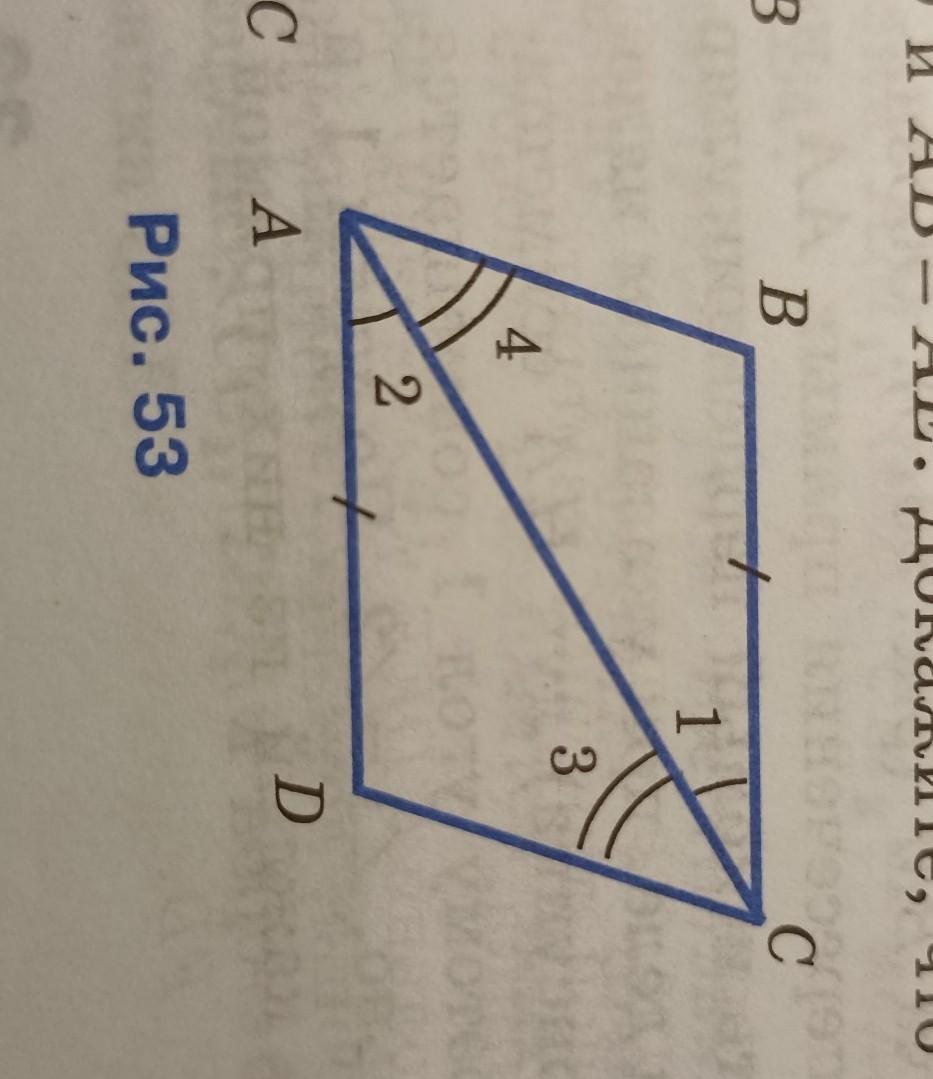
На рисунке 53 (см. с. 31) ВС=АD, АВ=СD. Докажите, что угол В = углу D ​

Answer 1

Ответ:

Объяснение:

Рассмотрим треугольник ABC и треугольник ADC, у них:

1) АС = АС (общая сторона)

2) угол 1 = углу 2 (как накрест лежащие для BC//AD, AC - секущая)

3) угол 3 = углу 4 (как накрест лежащие для CD//AB, AC - секущая)

Отсюда следует, что треугольники равны по стороне и двум прилежащим к ней углам. Тогда угол B=углу D как равные элементы ч.т.д