как ето решить? напишите на листе бумаги с объяснением
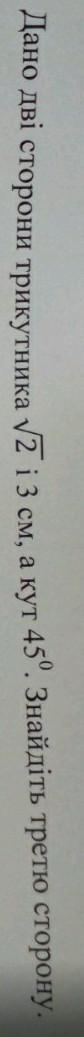
Ответы
если угол 45° лежит между этими сторонами, то применим теорему косинусов, если же против одной из сторон, то во всех случаях понимаем, что против большего угла должна лежать большая сторона.
1. b²=a²+c²-2a*c*cosβ- теорема косинусов.
по теореме косинусов третья сторона х равна
х=√(2+9-2*3*√2*сos 45°)=√(11-(2*3*√2*√2/2))=√(11-6)=√5≈2.24
такой треугольник существует. т.к. √2≈1.41; √5≈2.24, и третья сторона 3, неравенство треугольников выполняется.
1.41+2.24>3
2.24+3>1.41
1.41+3>2.24
если угол 45° не лежит между этими сторонами, а лежит против стороны 3,
то получим х²-2х*3*сos45°+2=9; х²-2х*3*√2*√2/2+2=9; х²-6х+9=0; (х-3)²=0; откуда х=3, а углы при стороне √2, окажутся равными по (180°-45°)/2=67.5°, т.к. стороны, содержащие угол 45° оказались равными.
треугольник этот существует. т.к. все три неравенства треугольника выполняются и все согласуется с условием, против большей стороны лежит больший угол.
если же угол 45° лежит против стороны √2 см, то
9+х²-2*х*3√2*/2=2
х²-х*3√2-2=0⇒х=1.5√2±√(2.25*2+2)=х=1.5√2±√6.5;
х=1.5√2-√6.5 не имеет смысла, поскольку не может сторона быть отрицательной; если х=1.5√2+√6.5≈4.67, такой треугольник не существует, т.к. 1.41+3<4/67, т.е. не выполняется неравенство треугольника.
Значит. задача имеет два решения. третья сторона или √5 см, или 3 см.