Предмет: Геометрия,
автор: 2ni8sher
Напиши уравнение окружности, которая проходит через точку 8 на оси Ox и через точку 10 на оси Oy, если известно, что центр находится на оси Oy.
(Дроби максимально сократите. Если в ответе получилось целое число, то запишите его в виде дроби со знаменателем 1.)
Приложения:
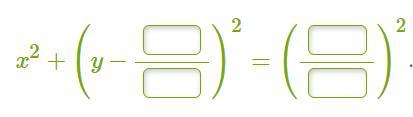
Ответы
Автор ответа:
1
Ответ: х²+(у-(9/5))²=(41/5)²
Объяснение:
т.е. проходит через точки (8;0) и (0; 10), раз ее центр на оси ОУ, то х₀=0.
Уравнение окружности с центром (х₀;у₀) и радиусом R, имеет вид
(х-х₀)²+(у-у₀)²=R² , значит, т.к. точки (8;0) и (0; 10) лежат на окружности, то удовлетворяют ее уравнению(8;0) и (0; 10), .
(8-0)²+(0-у₀)²=R²
(0-0)²+(10-у₀)²=R²
приравняв левые части, получим 64+у₀²=100-20у₀+у₀²⇒20у₀=100-64;
у₀=36/20=9/5, найдем теперь радиус. 64+у₀²=R²⇒R²=64+81/25=1681/25=
(41/5)²
Искомое уравнение окружности х²+(у-(9/5))²=(41/5)²
Похожие вопросы
Предмет: Английский язык,
автор: saxzade17
Предмет: Русский язык,
автор: Виктория12121212
Предмет: Русский язык,
автор: angelinar20001
Предмет: Физика,
автор: Аноним
Предмет: Физика,
автор: BasketballGrand