Question

Написать уравнение прямой, по которой плоскость x - 2y + 1 = 0 перемекает координатную плоскость 0xz

Answer 1

Написать уравнение прямой, по которой плоскость x - 2y + 1 = 0 пересекает координатную плоскость 0xz.

Если в общем уравнении плоскости Ax + By + Cz +D = 0  коэффициент C равен 0 (то есть Ax+By+D = 0), то эта плоскость параллельна оси Oz.

Поэтому линия пересечения плоскостей параллельна оси Oz.

Данная плоскость x – 2y + 1 = 0 пересекает ось Ох в точке (-1; 0; 0).

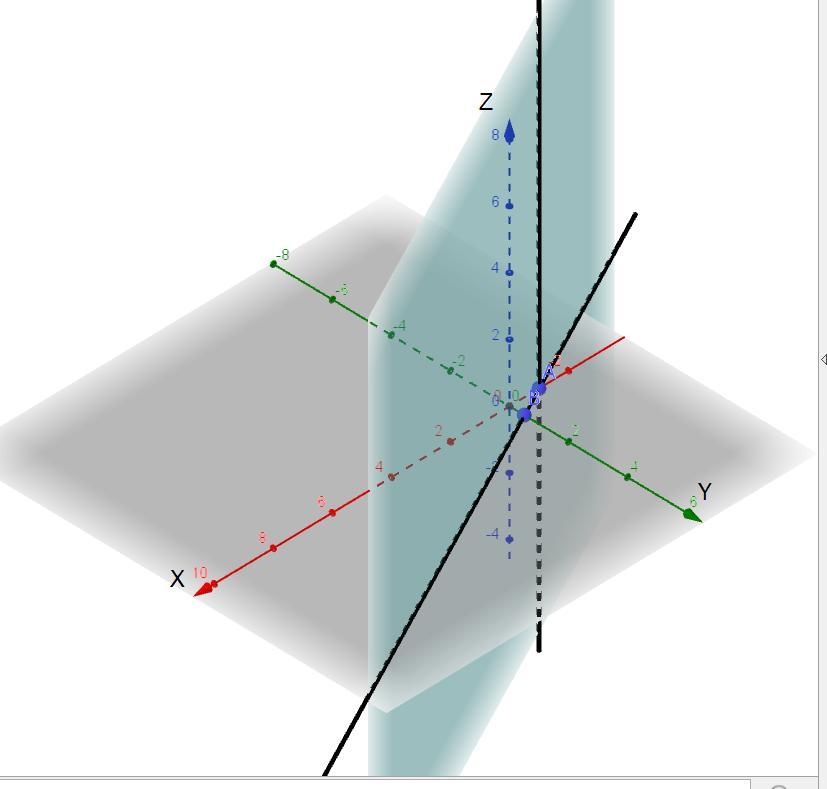
Так как прямая, канонические уравнения которой нам требуется составить, параллельна координатной оси Oz, то ее направляющим вектором является вектор z(0; 0; 1). Тогда канонические уравнения этой прямой в пространстве имеют вид  (x+1)/0=y/0=z/1.

Ответ:  (x+1)/0=y/0=z/1.